Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α, содержащей прямую BD1 и параллельной прямой AC,
является ромб.

а) Докажите, что грань ABCD — квадрат.

б) Найдите угол между плоскостями α и BCC1
, если AA1 =6, AB=4.

(108/145)

294

458

Посмотреть ответы 2

Ответы на вопрос:

marches

Геометрия

4,6(87 оценок)

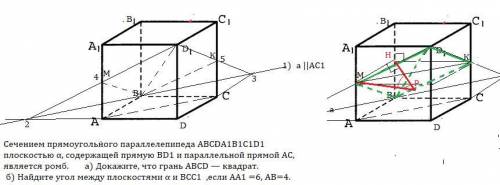
Сечением прямоугольного параллелепипеда ABCDA1B1C1D1

плоскостью α, содержащей прямую BD1 и параллельной прямой AC,

является ромб. а) Докажите, что грань ABCD — квадрат. б) Найдите угол между плоскостями α и BCC1 , если AA1 =6, AB=4.

Объяснение:

а) Проведем а||АС, значит а параллельна диагональному сечению АСС₁А₁⇒ МК||АС.

По условию BMD₁К-ромб, значит D₁В⊥МК по свойству диагоналей ромба и МК||АС. Тогда по т. о 3-х перпендикулярах : если наклонная D₁В перпендикулярна прямой лежащей в плоскости АС , то и проекция DВ⊥АС ( прямой , лежащей в плоскости ). Получили , что в прямоугольнике АВСD диагонали АС⊥DВ ⇒ АВСD -квадрат.

б)Проведем через М и К ( середины ребер) плоскость β║(АВС) , получим точку Н на ребре ВВ₁ , ВН=НВ₁=3 .

Пусть НР⊥ВК, т.к. МН⊥ВВ₁ ⇒ МР⊥ВК по т. о трех перпендикулярах⇒∠МРН-линейный угол данного двугранного.

ΔВНК -прямоугольный, ВК=√(16+9)=5.

ΔВНР≈ΔВНК ( по 2 углам общему и прямому) , значит сходственные стороны пропорциональны :

НР:НВ=НК:ВК , НР:3=4:5 , НР=12/5.

ΔМНР -прямоугольный , tg∠МРН=МН:РН , tg∠МРН=20/12=5/3

∠МРН=аrctg(5/3).

Сечением прямоугольного параллелепипеда ABCDA1B1C1D1 плоскостью α, содержащей прямую BD1 и параллель

znanijacom77

Геометрия

4,8(28 оценок)

собственно ответ вот не благодарите дада

В равнобедренном треугольнике боковая сторона равна 6, а высота проведённая к основанию, равна 4. На

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.