Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Выберите четную функцию: y=x^5−7/x^3 y=x^3 f(x)=2/x^2+x^8 областью определения...
 vlad080525.03.2023 18:29
vlad080525.03.2023 18:29 -
Периметр равнобедренного треугольника равен 1 м, а основание равна 0, 4 м...
 danilohca22.11.2022 13:35
danilohca22.11.2022 13:35 -
Запишите в стандартном виде числа: а) 89 200 б) 0,000473 в) 603,4*10(в 19...
 NaStYтуут13.11.2021 14:35
NaStYтуут13.11.2021 14:35 -
Решите уравнение икс шестых минус два икс третьих плюс три икс равно минус...
 DenchikKing11.10.2022 10:20
DenchikKing11.10.2022 10:20 -
6х+3у+18=0 8х-3у-24=0 ! заранее !...
 Соня234015.09.2020 07:59
Соня234015.09.2020 07:59 -
Иррациональное уравнение. 1.квадратный корень из 2x+5=2x-1 2.квадратный корень...
 МаркЛеткеман09.04.2020 03:43
МаркЛеткеман09.04.2020 03:43 -
Найдите смежные углы hk u kl если: а)угол hk меньше угла kl на 40 градусов...
 JHopeЧонХосочек02.12.2022 16:33
JHopeЧонХосочек02.12.2022 16:33 -
Легковые автомобили составляют 60% всего транспорта автопарка 90% из них автомобили...
 mira13327.09.2022 12:02
mira13327.09.2022 12:02 -
У х-5) во второй степени+(х-4)(-х-4)+(х-3)(х+7)...
 yanalatina9707.11.2021 05:52
yanalatina9707.11.2021 05:52 -
Дан вектор а модуль которого равен √5 изветстно что а (х;-2 ) найти х...
 antochakakaka29.04.2023 19:26
antochakakaka29.04.2023 19:26

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

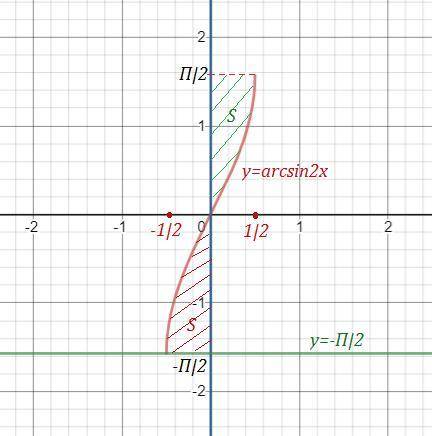
![y=arcsin2x\ \ ,\ \ x=0\ \ ,\ \ y=-\dfrac{\pi}{2}\\\\-1\leq 2x\leq 1\ \ \to \ \ -\dfrac{1}{2}\leq x\leq \dfrac{1}{2}\ \ ,\ \ \ -\dfrac{\pi}{2}\leq arcsin2x\leq \dfrac{\pi }{2}\\\\\\S=\int\limits_0^{1/2}\Big(\dfrac{\pi}{2}-arcsin2x\Big)\, dx=\int \limits _0^{1/2}\dfrac{\pi}{2}\, dx-\int\limits_0^{1/2}\, arcsin2x\, dx=\\\\\\=\Big[u=arcsin2x\ ,\ du=\dfrac{2\, dx}{\sqrt{1-4x^2}}\ ,\ dv=dx\ ,\ v=x\ \Big]=](/tpl/images/3779/7930/b1e50.png)
![=\dfrac{\pi}{2}\cdot x\Big|^{1/2}_0-x\cdot arcsin2x\Big|^{1/2}_0+\int\limits_0^{1/2}\, \dfrac{2x\, dx}{\sqrt{1-4x^2}}=\Big[\ d(1-4x^2)=-8x\, dx\ \Big]=\\\\\\=\dfrac{\pi}{2}(0+\dfrac{1}{2})-\dfrac{1}{2}\cdot arcsin1-\dfrac{1}{4}\int\limits_0^{1/2}\, \dfrac{d(1-4x^2)}{\sqrt{1-4x^2}}dx=\\\\\\=\dfrac{\pi}{4}-\dfrac{\pi}{4}-\dfrac{1}{4}\cdot 2\sqrt{1-4x^2}\Big|^{1/2}_0=-\dfrac{1}{2}\cdot (0-\sqrt1)=\dfrac{1}{2}](/tpl/images/3779/7930/07285.png)