Регистрация Спросить otvet5GPT
tsvirko7891
11.01.2020 02:56
Алгебра
Есть ответ 👍

3) Найдите значение выражения 2хо–уо, если (хо; уо) – решение системы уравнений: y= 2корень(x+3)
y+ 2= |x+2|

Заранее

211
485
Посмотреть ответы 3

Ответы на вопрос:

alina20021982
alina20021982
4,6(73 оценок)

...............................


3) Найдите значение выражения 2хо–уо, если (хо; уо) – решение системы уравнений: y= 2корень(x+3)y+ 2
deadraccoon20
deadraccoon20
4,7(98 оценок)
Решение:

Из второго уравнения системы выражаем 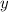y:

y = |x+2| - 2

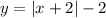
И подставляем в первое уравнение:

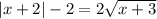
|x+2|-2=2\sqrt{x+3}

При этом нужно учитывать, что:

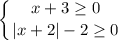
\displaystyle \left \{ {{x+3 \geq 0} \atop { |x+2|-2 \geq 0}} \right.

Из первого неравенства получаем, что 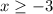x\geq -3.

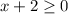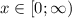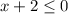Во втором неравенстве нужно рассмотреть два случая: при x+2 \geq 0 имеем, что x \in [0;\infty), при x+2 \leq 0 получаем, что x \in (-\infty;-4]. В итоге x \in ( - \infty; -4 ] \cup [0; + \infty).

В итоге получаем пересечение 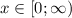x \in [0; \infty).

Учитывая это, возводим обе части полученного ранее уравнения в квадрат и раскрываем модули:

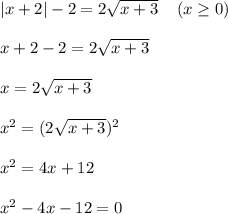
|x+2|-2 = 2\sqrt{x+3} \;\;\;\; (x \geq 0)\\\\x+2-2=2\sqrt{x+3} \\\\x = 2 \sqrt{x+3} \\\\x^2 = (2\sqrt{x+3} )^2 \\\\x^2 = 4x + 12\\\\x^2 - 4x - 12 = 0

При теоремы Виета получаем, что:

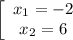
\left[\begin{array}{ccc}x_1=-2\\x_2=6\end{array}\right

Первый корень не удовлетворяет нас по введенным ограничениям, так что 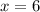x=6.

Найдем 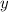y:

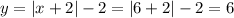
y = |x+2|-2 = |6+2|-2=6

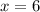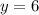Получаем, что x=6 и y=6. Эта пара удовлетворяет и первому уравнению, как можно убедиться.

Так что:

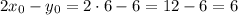
2x_0-y_0 = 2 \cdot 6 - 6 = 12-6=6

Задача решена!

ответ: 6.
Fat9l
Fat9l
4,5(62 оценок)

Объяснение:

шевщнашечшев

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS