Регистрация Спросить otvet5GPT
vikhrovdavid
17.11.2022 18:06
Алгебра
Есть ответ 👍

При каких значениях параметра a уравнение 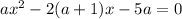ax^{2} -2(a+1)x-5a=0 имеет, по крайней мере, одно положительное решение

251
257
Посмотреть ответы 2

Ответы на вопрос:

missg78
missg78
4,8(29 оценок)

Проверим 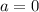a=0:  имеем уравнение 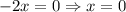-2x=0\Rightarrow x=0 - очевидно, не положительное решение, поэтому данное значение параметра не пойдет в ответ.

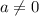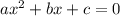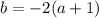При a\neq 0 уравнение - квадратное вида ax^2+bx+c=0 . Коэффициенты: a=a (внезапно), b=-2(a+1), c=-5a. Уравнение должно иметь корни по условию, т.е. его дискриминант как минимум не должен быть меньше 0.

Ищем дискриминант:

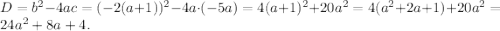
D=b^2-4ac=(-2(a+1))^2-4a\cdot(-5a)=4(a+1)^2+20a^2=4(a^2+2a+1)+20a^2=24a^2+8a+4.

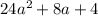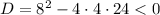
Найдем дискриминант трехчлена 24a^2+8a+4 : D=8^2-4\cdot4\cdot24<0

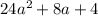
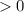Это значит что при любых a выражение 24a^2+8a+40, т.е. исходное уравнение всегда имеет 2 корня.

Могут быть три ситуации: 1) оба корня отрицательные; 2) корни имеют разные знаки; 3) оба корня положительные. Условию (нужно как минимум одно положительное решение) удовлетворяют только 2 и 3.

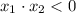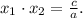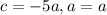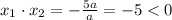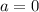Проверим второй случай. Если корни имеют разные знаки, то достаточно условия x_1\cdot x_2<0. По теореме Виета x_1\cdot x_2=\frac{c}{a}. Так как в нашем случае c=-5a, a=a, то x_1\cdot x_2=-\frac{5a}{a}=-5<0 при любых a. Т.е. при любых значениях параметра (кроме a=0) корни имеют разные знаки. Т.е. 3 случай уже можно не рассматривать, так как оба корня не могут быть положительными.

Значит, нас устраивают любые a, кроме a=0.

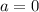ОТВЕТ: при 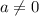a\neq 0.

Eva345678
Eva345678
4,8(66 оценок)
81^log(3)2=3^4log(3)2=3^log(3)16=16

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS