Математика: решить хоть что нибудь у меня пол часа заранее

Иленьк

30.09.2022 19:01

Математика

Есть ответ 👍

решить хоть что нибудь
у меня пол часа
заранее

254

257

Посмотреть ответы 3

Ответы на вопрос:

БоняЛизякин

Математика

4,4(88 оценок)

1. х=у=1

2^(x-y)=8

x=y=1

2^(x-y)=2^3

x=y=1

x-y=3

x=3+y

3+y=y=1

y=-2

x=3+(-2)=1

Пошаговое объяснение:

uciviyciy

Математика

4,4(58 оценок)

17.

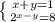
$\left \{ {{x+y=1} \atop {2^{x-y}=8}} \right.$

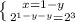
$\left \{ {{x=1-y} \atop {2^{1-y-y}=2^{3}}} \right.$

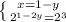
$\left \{ {{x=1-y} \atop {2^{1-2y}=2^{3}}} \right.$

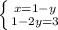
$\left \{ {{x=1-y} \atop {1-2y}=3}} \right.$

1-2y=3

-2y = 3 - 1

-2y = 2 | : (-2)

y = -1

x = 1 - (-1) = 1+1 = 2

ответ: (2;-1)

18.

2 sin²x + 5 cos x + 1 = 0

Из основного тригонометрического тождества sin²x + cos²x = 1 выразим sin²x

sin²x = 1-cos²x

2 * (1-cos²x) + 5 cos x + 1 = 0

2-2cos²x + 5 cos x + 1 = 0 | :(-1)

2cos²x - 5 cos x - 3 = 0

Пусть cos x=t, тогда

2t² - 5t - 3 = 0

D = (-5)² - 4*2*(-3) = 25 + 24 = 29 = 7²

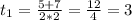
$t_{1} = \frac{5+7}{2*2} = \frac{12}{4} = 3$

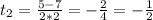
$t_{2} = \frac{5-7}{2*2} = -\frac{2}{4} = -\frac{1}{2}$

Вернёмся к замене:

Т.к. в уравнении cos x = a есть условие, что |a|≤1, то используем только второй корень

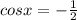
$cos x = - \frac{1}{2}$

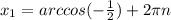$x_{1} = arccos (-\frac{1}{2}) + 2\pi n$ , n∈Z

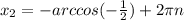$x_{2} = -arccos (-\frac{1}{2}) + 2\pi n$ , n∈Z

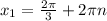$x_{1} = \frac{2\pi }{3} + 2\pi n$ ,n∈Z

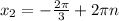$x_{2} = -\frac{2\pi }{3} + 2\pi n$ ,n∈Z

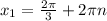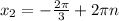ответ: $x_{1} = \frac{2\pi }{3} + 2\pi n$ ,n∈Z ; $x_{2} = -\frac{2\pi }{3} + 2\pi n$ ,n∈Z

vasa2283

Математика

4,4(66 оценок)

А) 4/5 : 3/4 =4/5*4/3=16/15 б) 6/7 : 2/5 =6/7*5/2=сократим 6 и 2=3/7*5=15/7 в) 4/9 : 1/2 =4/9*2=8/9 г) 7/12 : 8/11 =7/12*11/8=77/96

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.