Регистрация Спросить otvet5GPT
MyNameIsLiza123
10.09.2022 19:02
Математика
Есть ответ 👍

1) x^2y'+y^2=0, если y=1 при x=-1 2) xy'+y=3
3) xy'+y=x+1, y(1)=0
4) xy'-y=3
5) y''-4y'+3y=0
6) ay''+by'+cy=d , a=3, b=5, c=2, d=8, y(0)=6, y'(0)=-4

183
386
Посмотреть ответы 2

Ответы на вопрос:

nastyak12119
nastyak12119
4,7(75 оценок)

Пошаговое объяснение:

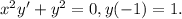
1) x^2y' +y^2 = 0, y(-1)=1.

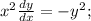
x^2\frac{dy}{dx} = -y^2;

Разделим переменные. При этом мы можем потерять решение 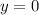y=0, но т.к. оно не удовлетворяет дополнительному условию, то оно не будет являться искомым решением.

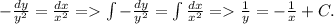-\frac{dy}{y^2}=\frac{dx}{x^2} = \int -\frac{dy}{y^2}=\int \frac{dx}{x^2} = \frac{1}{y} = -\frac{1}{x}+C. Используем дополнительное условие для определения константы:

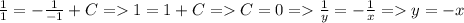
\frac{1}{1}=-\frac{1}{-1} + C = 1 = 1 +C = C =0 = \frac{1}{y} = -\frac{1}{x} = y=-x

ответ: 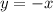y=-x

2) 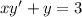xy'+y=3. Так как это уравнение является линейным неоднородным, то решение можно искать в виде суммы общего решения линейного однородного уравнения и частного решения неоднородного уравнений: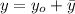 y=y_o +\bar y

Рассмотрим однородное уравнение:

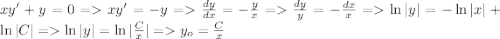
xy'+y = 0 = xy'=-y = \frac{dy}{dx}=-\frac{y}{x} = \frac{dy}{y}=-\frac{dx}{x} = \ln|y|=-\ln|x|+\ln|C| = \ln|y|=\ln|\frac{C}{x}| = y_o=\frac{C}{x}

(модули можно опустить без знака плюс-минус в следствие произвольности постоянной С. При делении на y мы могли потерять решение y=0, но оно входит в семейство кривых при С=0)

Частное решение неоднородного уравнения легко угадывается: 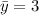\bar y= 3

Следовательно, общее решение исходного уравнения: 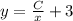y = \frac{C}{x} + 3

ответ: 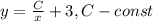y=\frac{C}{x}+3, C - const

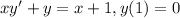
3) xy' + y = x+1, y(1) =0

Данное уравнение отличается от предыдущего только неоднородностью, поэтому нужно просто подобрать другое частное решение, удовлетворяющее неоднородности. Имеет смысл ее искать в виде: 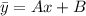\bar y= Ax+B, подставим его в уравнение:

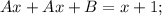
Ax + Ax + B = x +1;

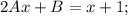
2Ax + B = x + 1;

Два полинома тождественно равны, если равны коэффициенты при соответствующих степенях:

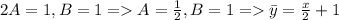
2A = 1, B=1 = A=\frac{1}{2}, B=1 = \bar y = \frac{x}{2}+1

Следовательно, общее решение исходного уравнения: 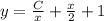y= \frac{C}{x} +\frac{x}{2}+1

Найдем константу из дополнительного условия:

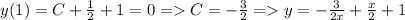
y(1)=C + \frac{1}{2}+1 = 0 = C = -\frac{3}{2} = y=-\frac{3}{2x}+\frac{x}{2}+1

ответ: 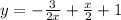y=-\frac{3}{2x}+\frac{x}{2}+1

4) xy'-y=3.

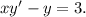
Применим алгоритм из пункта 2

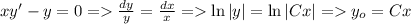
xy'-y = 0 = \frac{dy}{y}=\frac{dx}{x} = \ln|y|=\ln|Cx| = y_o=Cx

Частное решение неоднородного уравнения легко угадывается: 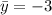\bar y = -3

Следовательно, общее решение исходного уравнения: 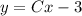y= Cx-3

ответ: 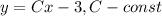y=Cx-3, C - const

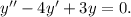
5) y''-4y'+3y=0.

Имеем дело с линейным однородным уравнением с постоянными коэффициентами. Его частные решения ищутся в виде: 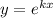y = e^{kx}. Тогда характеристическое уравнение есть

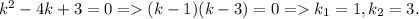
k^2-4k+3 =0 = (k-1)(k-3) =0 = k_1=1, k_2=3.

Общее решение такого уравнения записывается в виде линейной комбинации линейно независимых частных решений, экспоненты с неравными показателями являются линейно независимыми:

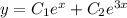
y=C_1e^x+C_2e^{3x}

ответ: 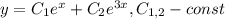y=C_1e^x+C_2e^{3x}, C_{1,2} - const

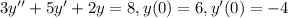
6) 3y''+5y'+2y=8, y(0)=6, y'(0)=-4

Общее решение является суммой общего решения однородного уравнения и частного решения неоднородного. Рассмотрим однородное: 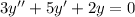3y''+5y'+2y=0

Характеристическое уравнение: 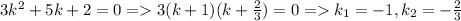3k^2+5k+2=0 = 3(k+1)(k+\frac{2}{3})=0 = k_1=-1, k_2=-\frac{2}{3}

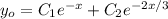
y_o = C_1e^{-x} + C_2e^{-2x/3}

Частное решение легко угадывается: 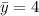\bar y = 4

Общее решение: 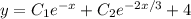y= C_1e^{-x}+C_2e^{-2x/3}+4

Определим постоянные из дополнительных условий:

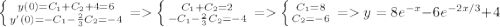
\left \{ {{y(0)=C_1+C_2+4=6} \atop {y'(0)=-C_1-\frac{2}{3}C_2 = -4}} \right. = \left \{ {{C_1+C_2=2} \atop {-C_1-\frac{2}{3}C_2 = -4}} \right. = \left \{ {{C_1=8} \atop {C_2=-6}} \right. = y = 8e^{-x} -6e^{-2x/3}+4

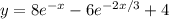
ответ: y=8e^{-x}-6e^{-2x/3}+4

hdjdhd1
hdjdhd1
4,5(49 оценок)
Две бригады маляров красят помещения в здании. 1 бригада за 6 дней израсходовала 72кг краски. 2 бригада израсходовала 60 кг краски, причем обе бригады расходовали одинаковое количество краски в день. сколько дней работала 2 бригада? решение: 72: 6=12 (кг/д) расходует 1 бригада 60: 12=5 (д) ответ: вторая бригада работала 5 дней

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS