Ангелина0611

30.01.2023 23:37

Геометрия

Есть ответ 👍

По данной стороне основания 9 и боковому ребру 6 найти площадь полной поверхности правильной треугольной пирамиды.

237

251

Посмотреть ответы 2

Ответы на вопрос:

Толиk

Геометрия

4,5(41 оценок)

Дано:

Правильная треугольная пирамида.

АС = 9

SC = 6

Найти:

S полн поверхности - ?

Решение:

Так как данная пирамида - правильная треугольная => основание этой пирамиды - равносторонний треугольник.

Равносторонни треугольник - треугольник, у которого все углы и стороны равны.

=> АВ = ВС = АС = 9

S равностороннего △ = а²√3/4, где а - сторона треугольника.

S равностороннего △ = 9²√3/4 = 81√3/4 ед.кв.

S боковой поверхности = 1/2(Р осн + L), где Р - периметр основания; L - апофема.

Апофема - высота боковой грани правильной пирамиды, проведённая из её вершины.

SR - апофема

Р = (АВ + ВС + АС)/2 = (9 * 3)/2 = 13,5

Апофема делит сторону основания на 2 равные части.

Так как ВС = 9 => BR = RC = 9/2 = 4,5

△SRC - прямоугольный, так как SR - высота.

Найдём апофему SR, по теореме Пифагора: (с = √(a² + b²), где с - гипотенуза; а, b - катеты)

SR = √(SC² - RC²) = √(6² - (4,5)²) = 3√7/2

S боковой поверхности = (13,5 + 3√7/2)/2 = 27 + 3√7/4 ед.кв.

S полной поверхности = S основания + S боковой поверхности = 81√3/4 + 27 + 3√7/4 = 3/4 * (27√3 + 9 + √7) ед.кв.

ответ: 3/4 * (27√3 + 9 + √7) ед.кв.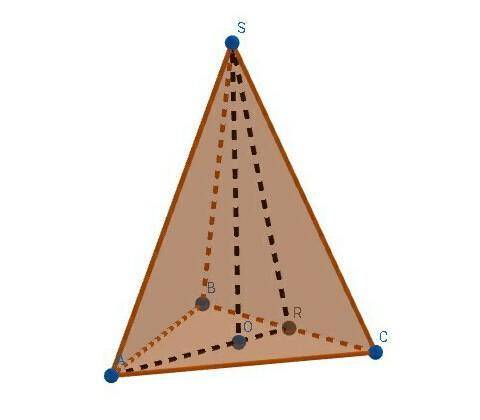
По данной стороне основания 9 и боковому ребру 6 найти площадь полной поверхности правильной треугол

LEXSUS18

Геометрия

4,8(42 оценок)

угл 1=угл 4=123-вертикальные

угл 5=угл 8=63-вертикальные

угл 8= угл 2=63-накрест лежащие

угл 2= угл 3=63-вертикальные

угл 4=угл 6=123-накрест лежащие

угл 6=угл7=123-вертикальные

угл1=123

угл2=63

угл3=63

угл4=123

угл5=63

угл6=123

угл7=123

угл8=63

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.