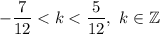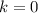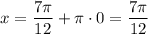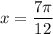Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Алгебра хелп скрины предложила,8 класс 15 балов...
 www2204200401.02.2021 16:33
www2204200401.02.2021 16:33 -
Найдите значение выражения (2+х)(х²-2х+4)-1+х³ при х...
 никто27203.06.2022 00:06
никто27203.06.2022 00:06 -
Oneepcmus 40 20 20 Чертеж 27.10....
 assel0003119.11.2021 13:07
assel0003119.11.2021 13:07 -
КЛАСС. Решите уравнение, используя правила разложения на множители...
 prunsesca00521.01.2021 15:23
prunsesca00521.01.2021 15:23 -
Решите уравнение: (12.5-х): 5=(3.6+х): 6...
 alibaevaalina14625.10.2020 14:26
alibaevaalina14625.10.2020 14:26 -
Как делить обычное число на проценты?...
 danyok13200617.12.2022 03:15
danyok13200617.12.2022 03:15 -
Постройте график функции y=sin(x-pi/3) решите на листок и сфоткайте...
 jokjok133701.08.2020 20:54
jokjok133701.08.2020 20:54 -
Выполнить действия б) (7m^2-20mn-10m): 10m=...
 Semen91112.05.2021 16:00
Semen91112.05.2021 16:00 -
1) дачный участок имеет форму квадрата , стороны которого равны...
 Vova5202631.12.2022 11:18
Vova5202631.12.2022 11:18 -
Сторона ас треугольника авс проходит через центр описанной около...
 7918551930519.01.2023 02:43
7918551930519.01.2023 02:43

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

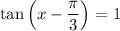
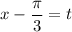
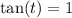
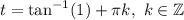
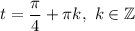
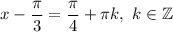
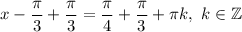
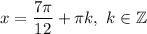
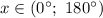 i. e.
i. e. 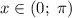 then:
then: