Sunlight11

15.06.2020 15:57

Есть ответ 👍

Боковые стороны прямоугольной трапеции равны 17 и 8, а её основание относятся как 2:5. Найдите площадь трапеции

293

495

Посмотреть ответы 3

Ответы на вопрос:

Школьник7555

Геометрия

4,7(93 оценок)

И сразу после последней записи на фото пиши:

S трапеции = ср.линия * h = 23+8/2 * 8 = 15.5 * 8 = 124 см^2

Vova89898

Геометрия

4,5(72 оценок)

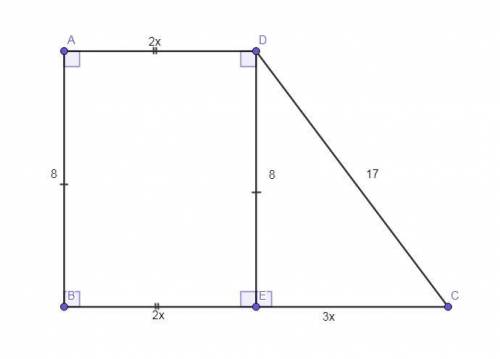
Проведём из вершины угла ∠ADC высоту DE на основание ВС трапеции ABCD. По свойству прямоугольной трапеции она равна меньшей боковой стороне АВ.

Пусть основание AD = 2х, тогда основание ВС = 5х.

Рассмотрим четырёхугольник ABED. У него все углы прямые, значит, четырёхугольник ABED - прямоугольник.

Противоположные стороны прямоугольника равны. АD = ВЕ = 2х. Следовательно, отрезок основания ЕС = 5х-2х = 3х.

Рассмотрим прямоугольный ΔDEC.

По теореме Пифагора -

DE²+EC² = DC²

EC² = DC²-DE²

Подставим в формулу известные нам значения -

(3х)² = 17²-8²

9х² = 289-64

9х² = 225

х² = 25

х₁ = -5 - не удовлетворяет условию.

х₂ = 5 - подходит.

Площадь трапеции равна полусумме её оснований и высоты.

Полусумма оснований = 0,5*(2х+5х) = 0,5*(2*5+5*5) = 0,5*(10+25) = 17,5.

Высота = 8.

Площадь трапеции = 17,5*8 = 140 (ед²).

ответ: 140 (ед²).

Djamila1108

Геометрия

4,6(45 оценок)

S=0,5•h•10 h-высота h=10•sin60°=10√3\2=5√3 s=25√3 ответ: 25

Задай свой вопрос

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.