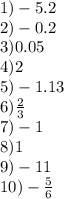Ответы на вопрос:
F(x)=-x³+3x²-4. 1. область определения функции: x∈r (функция определена на x∈(-∞; +∞). 2. четность/нечетность: f(-x)=)³+3(-x)²-4=x³+3x²-4≠f(x)≠-f(x) - функция ни четная, ни нечетная. 3. непрерывность: функция непрерывна на всей области определения. 4. поведение функции при x→+-∞: при x→-∞, f(x)→+∞; при x→+∞, f(x)→-∞. 5. производная функции: f'(x)=(-x³+3x²-4)'=-(x³)'+3*(x²)'-4'=-3x²+3*2x-0=-3x²+6x. 6. экстремумы функции: f'(x)=0, -3x²+6x=0 ⇒ x²-2x=0 ⇒ x(x-2)=0 ⇒ x=0 и x=2. 7. монотонность (промежутки возрастания и убывания) функции: при x∈(-∞; 0], f'(x)< 0 - функция убывает, при x∈[0; 2], f'(x)> 0 - функция возрастает, при x∈[2; +∞), f'(x)< 0 - функция убывает. следовательно x=0 - точка минимума, x=2 - точка максимума. 8. пересечение графика функции с осями координат: с осью абсцисс, f(x)=0 ⇒ -x³+3x²-4=0 ⇒ x=-1 и x=2, получим точки (-1; 0) и (2; 0); с осью ординат, x=0, f(x)=-4, получим точку (0; -4). 9. строим график (см. в приложении)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Выражения: а) (y - 2)² + (1 + 2y)² б) (7 - 8x)(8x + 7) в) (a - 2)(a²...
 korablevabella25.08.2021 21:23
korablevabella25.08.2021 21:23 -
Конкурс газет листовок на тему чем или кем знаменита франция...
 DashaDoro0303.11.2022 14:20
DashaDoro0303.11.2022 14:20 -
Разложите на множители 4a^2-4a-3b^2...
 denisprokopev03.02.2020 08:28
denisprokopev03.02.2020 08:28 -
По логарифму 1)решите систему 2)найдите промежутки возрастания и...
 albina23608.09.2021 03:48
albina23608.09.2021 03:48 -
Мне нужна найти значения выражения a-2b+c при a=1.3 b=-0.6 и c=-3.5...
 timbn200621.04.2022 07:07
timbn200621.04.2022 07:07 -
Решить известно что log 43 по основанию 1/4 =a найдите log 43/256...
 weelrockster08.06.2022 22:16
weelrockster08.06.2022 22:16 -
Поместится ли? Надо обосновать. ...
 malinka14011713.04.2021 08:43
malinka14011713.04.2021 08:43 -
Функция задана формулой y = 5х + 20 а)значение у если х=-0,8 б)значение...
 Gggg2563227.04.2023 07:46
Gggg2563227.04.2023 07:46 -
При каких значениях x дробь не определена? 14,65x3−18,6x2−4x+4....
 adadasda65p06utn27.09.2020 11:49
adadasda65p06utn27.09.2020 11:49 -
Найдите значение выражения: cos (3Pi-B) - sin (- 3Pi/2 + B) / 5 cos...
 Kimbra809.11.2021 16:20
Kimbra809.11.2021 16:20

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.