1. В остроугольном треугольнике:
• один угол острый, два других - любые
• сумма углов меньше суммы углов в прямоугольном или тупоугольном треугольнике
• все углы острые
• менее трех острых углов
2. В прямоугольном треугольнике:
• один из углов прямой, а два других острые и равны друг другу
• сумма острых углов равна 90°
• все углы прямые
• один из углов прямой, а другие могут быть как острыми, так и тупыми
3. Внешний угол треугольника:
• это угол, который равен сумме двух других углов
• это угол, который расположен вне данного треугольника
• это угол, градусная мера которого равна сумме градусных мер двух углов треугольника
• это угол, смежный с каким-нибудь углом этого треугольника
4. В треугольнике:
• против меньшего угла лежит большая сторона
• против большего угла лежит меньшая сторона
• против большей стороны лежит тупой угол
• против большей стороны лежит больший угол
5. Каждая сторона треугольника:
• равна сумме двух других его сторон
• больше суммы двух других его сторон
• меньше суммы двух других его сторон
• меньше или равна сумме двух других его сторон
6. В прямоугольном треугольнике:
• катет, лежащий против угла, равного 30°, составляет половину гипотенузы
• если гипотенуза равна половине катета, то данная гипотенуза лежит против угла, равного 30°
• катет, прилежащий к углу, равному 30°, составляет половину гипотенузы
• сумма любых двух углов равна 90°
7. Признак равенства прямоугольных треугольников:
• если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны
• если два угла одного прямоугольного треугольника соответственно равны двум углам другого, то такие треугольники равны
• если гипотенуза и угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого, то такие треугольники равны
• если две стороны одного прямоугольного треугольника соответственно равны двум сторонам другого, то такие треугольники равны
8. Расстоянием от точки до прямой называется:
• расстояние от данной точки до какой-нибудь точки данной прямой
• длина отрезка, проведенного из данной точки к данной прямой
• длина перпендикуляра, проведенного из данной точки к данной прямой
• длина отрезка, соединяющего данную точку с какой-нибудь точкой данной прямой
9. Какое из утверждений верно?
• наклонная совпадает с гипотенузой
• перпендикуляр, проведенный из точки к прямой, меньше любой наклонной, проведенной из той же точки к этой прямой
• перпендикуляр меньше любой из наклонных
• все наклонные, проведенные изданной точки к данной прямой, равны
10. В равнобедренном треугольнике:
• внешний угол при основании не может быть тупым
• угол при вершине не может быть прямым
• угол при основании может быть острым или прямым
• угол при основании не может быть тупым

205

351

Посмотреть ответы 1

Ответы на вопрос:

alyonavasnecova34

Геометрия

4,8(60 оценок)

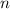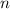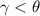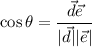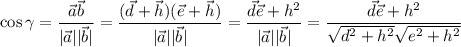Многогранный угол составлен боковыми сторонами -угольной пирамиды, в основании которой лежит выпуклый -угольник. Рассмотрим одну из таких сторон. Докажем, что $\gamma$ (см. рисунок). Тогда $\cos\theta = \dfrac{\vec{d}\vec{e}}{|\vec{d}||\vec{e}|}$ и $\cos\gamma = \dfrac{\vec{a}\vec{b}}{|\vec{a}||\vec{b}|} = \dfrac{(\vec{d}+\vec{h})(\vec{e}+\vec{h})}{|\vec{a}||\vec{b}|} = \dfrac{\vec{d}\vec{e}+h^2}{|\vec{a}||\vec{b}|} = \dfrac{\vec{d}\vec{e}+h^2}{\sqrt{d^2+h^2}\sqrt{e^2+h^2}}$ . Вот сейчас будет немного муторно: 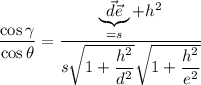$\dfrac{\cos\gamma}{\cos\theta} = \dfrac{\underbrace{\vec{d}\vec{e}}_{=s}+h^2}{s\sqrt{1+\dfrac{h^2}{d^2}}\sqrt{1+\dfrac{h^2}{e^2}}}$ . Однако 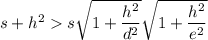$s+h^2 s\sqrt{1+\dfrac{h^2}{d^2}}\sqrt{1+\dfrac{h^2}{e^2}}$ , действительно, 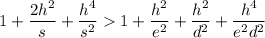$1+\dfrac{2h^2}{s}+\dfrac{h^4}{s^2}1+\dfrac{h^2}{e^2}+\dfrac{h^2}{d^2}+\dfrac{h^4}{e^2d^2}$ , что верно, поскольку каждое слагаемое слева (кроме единицы) больше соответствующего слагаемого справа. Поэтому 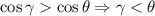$\cos\gamma \cos\theta \Rightarrow \gamma$ . Теперь спроецировав вершину 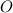многогранного угла на плоскость (многоугольник), получим, что сумма плоских углов меньше суммы углов при вершине 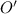проекции 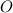, которая равна в точности 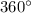$360^{\circ}$ , что и требовалось.

Докажите что сумма всех плоских углов выпуклого многогранного угла меньше 360 градусов

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.