Алгебра: РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ

sulti1675gmailcom

07.07.2022 08:03

Алгебра

Есть ответ 👍

РЕШИТЬ СИСТЕМУ УРАВНЕНИЙ

280

378

Посмотреть ответы 1

Ответы на вопрос:

foreveryoung5

Алгебра

4,8(1 оценок)

Понятно, что 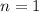n=1 не годится. Рассмотрим 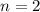n=2 . Пусть функция 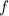такова, что 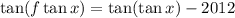$\tan(f\tan x)=\tan(\tan x)-2012$ (несложно показать, что такая существует). Тогда 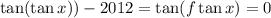$\tan(\tan x))-2012=\tan(f\tan x)=0$ , откуда 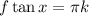$f \tan x=\pi k$ , наконец, 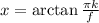$x=\arctan \frac{\pi k}{f}$ . При этом 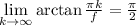$\lim\limits_{k\to\infty} \arctan \frac{\pi k}{f}=\frac{\pi}{2}$ . Поскольку 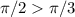$\pi/2\pi/3$ , то на указанном отрезке поместится только конечное количество членов последовательности.

Проводя аналогичные рассуждения (в этот раз берем функцию 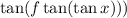$\tan(f\tan(\tan x)))$ ), получаем предел 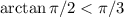$\arctan \pi/2$ (для доказательства достаточно взять тангенс от обеих частей). Значит, на указанном отрезке лежит бесконечное количество членов последовательности. Итак, ответ n=3 .

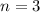Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.