Геометрия: нужно, там если что 2 треугольника надо решить.

arinakirkot

01.09.2021 10:05

Геометрия

Есть ответ 👍

нужно, там если что 2 треугольника надо решить.

168

230

Посмотреть ответы 2

Ответы на вопрос:

maks8707

Геометрия

4,8(25 оценок)

кароче , угол BEC = 30°

AEB= 120°

ABE=30 следовательно BC биссектриса , следовательно AE=EC = 7

personalyanaul

Геометрия

4,7(10 оценок)

S=40см², Р=4√2+20=29,64см

Объяснение:

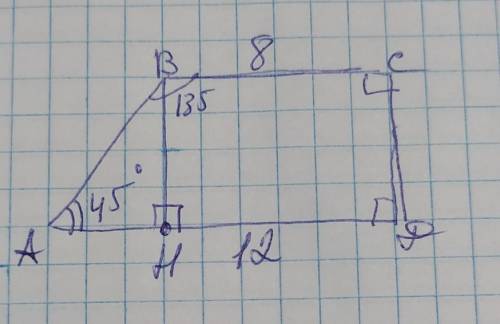
обозначим вершины трапеции А В С Д с основаниями ВС и АД и тупым углом В=135°. Так как сумма углов трапеции, прилегающих к одной боковой стороне составляет 180°, то <А=180–135=45°

Проведём к нижнему основанию АД высоту ВН. Она делит АД так что НД=ВС=8см, тогда АН=12–8=4см. Рассмотрим полученный ∆АВН. Он прямоугольный и АН и ВН катеты а АВ - гипотенуза. В прямоугольном треугольнике сумма острых углов составляет 90°, поэтому <АВН=90–45°=45°, значит <АВН=<А=45°, следовательно ∆АВН прямоугольный равнобедренный, поэтому АН=ВН=4см. Площадь трапеции вычисляется по формуле:

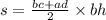
$s = \frac{bc + ad}{2} \times bh$

вставим в формулу наши данные:

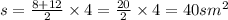
$s = \frac{8 + 12}{2} \times 4 = \frac{20}{2} \times 4 = 40sm {}^{2}$

Итак: S=40см²

Теперь в ∆АВН найдём гипотенузу АВ, которая является боковой стороной трапеции, по теореме Пифагора:

АВ²=АН²+ВН²=4²+4²=16+16=32; АВ=СД=√32=4√2см. Высота ВН=СД=4 см. Теперь найдём периметр трапеции зная её стороны: Р=4√2+8+12+4=4√2+24см

Если нужно вычислить полностью, то √2≈1,41, тогда:

Р=4×1,41+24=5,64+20=29,64см

Найдите периметр и площадь прямоугольной трапеции, основания которой составляют 8 см и 12 см, а углы

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.