Аяна1765

22.04.2023 20:48

Геометрия

Есть ответ 👍

Большее основание трапециив 3 раза больше меньшего.найдите основания трапеции,если средняя линия равна 20

147

296

Посмотреть ответы 3

Ответы на вопрос:

funisinfinity26

Геометрия

4,8(57 оценок)

меньшее основание х

большее основание 3х

(х+3х): 2=20

4х/2=20

2х=20

х=10 - меньшее основание;

3*10=30 - большее основание

ответ: меньшее основание 10; большее-30.

мопдркиопм

Геометрия

4,6(19 оценок)

ответ:

10 и 30.

объяснение:

сумма оснований равна 40.

пусть меньшее основание равна х,большее равно 3х

уравнение х+3х=40; 4х=40; х=10

3х=30

natalyazaprudsozxkk3

Геометрия

4,4(59 оценок)

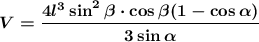
$\boldsymbol{V=\dfrac{4l^3\sin^2\beta\cdot \cos\beta (1-\cos\alpha)}{3\sin\alpha}}$

Объяснение:

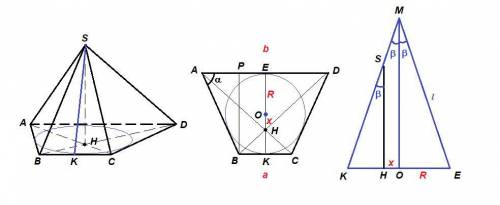
Центр окружности, вписанной в равнобедренную трапецию, лежит на середине отрезка КЕ (точки К и Е - середины оснований).

Так как точка пересечения диагоналей лежит на том же отрезке, но ближе к меньшему основанию, высота пирамиды лежит на образующей конуса, проходящей через точку К.

Высота трапеции равна диаметру вписанной окружности, а суммы противолежащих сторон равны.

Итак, ВР = КЕ = 2R,

AB + CD = AD + BC

AD = b, BC = a.

Чтобы найти высоту пирамиды, надо знать длину КН, а для этого найти расстояние между центром окружности и основанием высоты пирамиды ОН = х.

ΔАВР: ∠АРВ = 90°,

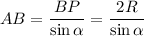
$AB=\dfrac{BP}{\sin\alpha}=\dfrac{2R}{\sin\alpha }$

AP = BP · ctg α = 2R · ctg α

Тогда

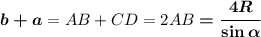
$\boldsymbol{b+a}=AB+CD=2AB\boldsymbol{=\dfrac{4R}{\sin\alpha}}$

Так как по свойству равнобедренной трапеции

АР = (AD - BC) / 2, то

b - a = 2AP = 4R · ctg α

ΔAHD ~ ΔCHB по двум углам, тогда их высоты относятся как сходственные стороны:

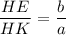
$\dfrac{HE}{HK}=\dfrac{b}{a}$

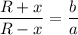
$\dfrac{R+x}{R-x}=\dfrac{b}{a}$

a(R + x) = b(R - x)

aR + ax = bR - bx

x(a + b) = R(b - a)

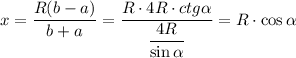
$x=\dfrac{R(b-a)}{b+a}=\dfrac{R\cdot 4R\cdot ctg\alpha}{\dfrac{4R}{\sin\alpha}}=R\cdot \cos\alpha$

KH = R - x = R(1 - cos α)

Справа на рисунке осевое сечение конуса, проходящее через хорду КЕ.

∠KSH = ∠KMO = β как соответственные при SH║MO и секущей КМ.

SH = KH · ctg β = R(1 - cos α) · ctgβ

Итак, объем пирамиды:

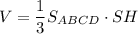
$V=\dfrac{1}{3}S_{ABCD}\cdot SH$

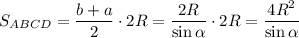
$S_{ABCD}=\dfrac{b+a}{2}\cdot 2R=\dfrac{2R}{\sin\alpha }\cdot 2R=\dfrac{4R^2}{\sin\alpha}$

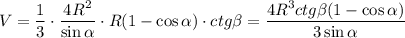
$V=\dfrac{1}{3}\cdot \dfrac{4R^2}{\sin\alpha }\cdot R(1-\cos\alpha )\cdot ctg\beta=\dfrac{4R^3ctg\beta (1-\cos\alpha)}{3\sin\alpha}$

Осталось из прямоугольного треугольника МОЕ выразить R:

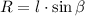
$R=l\cdot \sin\beta$

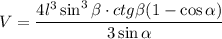
$V=\dfrac{4l^3\sin^3\beta\cdot ctg\beta (1-\cos\alpha)}{3\sin\alpha}$

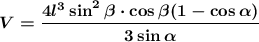
$\boldsymbol{V=\dfrac{4l^3\sin^2\beta\cdot \cos\beta (1-\cos\alpha)}{3\sin\alpha}}$

Основанием пирамиды служит равнобедренная трапеция с острым углом Эта трапеция описана около окружн

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.