otlichnik41

18.01.2021 17:01

Геометрия

Есть ответ 👍

Определите стороны параллелограмма его периметр равен 38 дм , а одна из сторон на 7 см меньше другой.

160

167

Посмотреть ответы 3

Ответы на вопрос:

Fuvhrcsghinm

Геометрия

4,6(93 оценок)

ответ:

объяснение:

одна сторона х

другая х+7

р=2(a+b)

2(x+x+7)=38

2(2x+7)=38

2x+7=38/2

2x+7=19

2x=19-7

2x=12

x=12/2

x=6 дм одна сторона

x+7=13 дм другая сторона

проверка

(6+13)*2=19*2=38

13-6=7

mirgin2002

Геометрия

4,4(85 оценок)

пусть одна сторона х/дм/, тогда другая /х+7/ дм, полупериметр равен 38/2=19,

2x+7=19;

2x=12

x=6; 6 дм одна сторона

x+7=13 /дм/ другая

LizaIvaskevich

Геометрия

4,4(52 оценок)

Решение с ответом:

AB = 12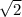 $\sqrt{2}$ см

BC = 20 см

A = 45 градусов

BM - h

------------------------

СМ = ? см

Высота BM является перпендикуляром, опущенным на AC.

Т.е угол BMA и угол BMC - прямоугольные ( 90 градусов)

расс-им прямоугольный треугольник ABM:

угол BAM = 45 градусов (из условия)

угол BMA = 90 градусов (BM - высота)

Найдем угол ABM по Теореме о сумме углов треугольника:

180 - (BAM + BMA) = 180 - (90 + 45) = 45 градусов.

Прямоугольный треугольник ABM является равнобедренным, его катеты равны м-у собой.

AM = BM

Гипотенуза у треугольника - AB, она равна 12 корень из 2 (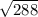 $\sqrt{288}$ )

Из Теоремы Пифагора (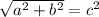 $\sqrt{a^2 + b^2 } = c^2$ ) выходит, что квадрат равных м-у собой катетов a и b равен 144, корень из 144 - 12.

т.е AM = BM = 12 см.

расс-им треугольник BMC:

угол BMC - также прямоугольный.

BM = 12 см (по решению)

BC = 20 cм (из условия)

Катет CM = ? см

Найдем его из Обратной Теоремы пифагора:

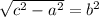
$\sqrt{c^2 - a^2} = b^2$

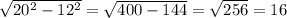$\sqrt{20^2 - 12^2} = \sqrt{400 - 144} = \sqrt{256} = 16$ см

ОТРЕЗОК CM РАВЕН 16 СМ.

Высота BM треугольника ABC делит его сторону АС на отрезки АМ и СМ. Найдите длину отрезка СМ, если А

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.