Укажите в ответе номера верных утверждений: 1 )центром вписанной окружности треугольника является точка пересечения его высот . 2)центром вписанной окружности треугольника является точка пересечения его медиан. 3) центром вписанной окружности является точка пересечения его биссектрис .4)центром описанной окружности треугольника является точка пересечения его высот. 5) центром описанной окружности треугольника является точка пересечения его медиан .6) центром описанной окружности треугольника является точка пересечения его биссектрис.

298

302

Посмотреть ответы 2

Ответы на вопрос:

Mamishbdjsnb

Геометрия

4,4(9 оценок)

3) центром вписанной окружности является точка пересечения его биссектрис. около треугольника можно описать окружность, притом только одну. её центром будет являться точка пересечения серединных перпендикуляров. такого ответа нет если только это не равносторонний треугольник тогда это точка пересечения его высот

gricenkoviktor

Геометрия

4,4(67 оценок)

Дано:

△CBA;

P△CBA = 45 мм;

CB = 15 мм

BA - CB - AC = 6 мм.

Найти:

BA = ? мм; AC = ? мм.

Решение:

Периметр треугольника это сумма всех длин сторон.

Пусть x мм - большая сторона, тогда y мм - меньшая сторона и средняя 15 мм.

→ Составим и решим систему уравнений:

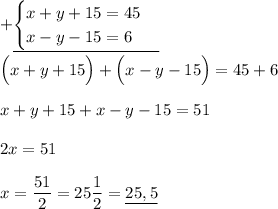
$+\underline{\begin{cases} x+y+15=45 \\ x-y-15=6\end{cases}} \\ \\ \Big(x+y+15\Big)+\Big(x-y-15\Big)=45+6 \\ \\ x+y+15+x-y-15=51 \\ \\ 2x = 51 \\ \\ x=\dfrac{51}{2}=25\dfrac{1}{2}=\underline{25,5}$

Если большая сторона BA составляет 25,5 мм, то меньшая AC будет равна 4,5 мм.

ответ: BA (большая) = 25,5 мм; АС (меньшая) = 4,5 мм.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.