Основанием прямой призмы abcda1b1c1d1 является ромб abcd, в котором большая диагональ ac=17см. объем призмы равен 1020см^3. через диагональ ac и вершину b1 тупого угла верхнего основания призмы проведена плоскость, образующая с плоскостью основания угол альфа. найдите площадь полученного сечения призмы (в см^2), если tg альфа = 2,4.
Ответы на вопрос:
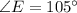
Проведём биссектрисы 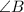 и
и 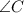 . Пусть они пересекаются в точке
. Пусть они пересекаются в точке 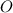 .
.
Также проведём прямые 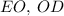 и
и 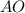 .
.
========================================
Рассмотрим 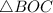 :
:
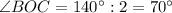 , т.к.
, т.к. 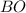 - биссектриса.
- биссектриса.
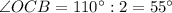 , т.к.
, т.к. 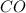 - биссектриса.
- биссектриса.
Сумма внутренних углов треугольника равна 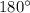 .
.
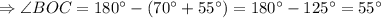
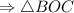 - равнобедренный.
- равнобедренный.
========================================
Рассмотрим 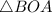 и
и 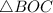 :
:
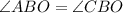 , т.к.
, т.к. 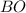 - биссектриса;
- биссектриса;
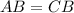 (по условию);
(по условию); 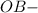 общая сторона.
общая сторона.
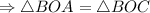 (по I признаку равенства треугольников).
(по I признаку равенства треугольников).
========================================
Рассмотрим 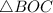 и
и 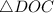 :
:
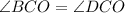 , т.к.
, т.к. 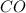 - биссектриса;
- биссектриса;
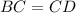 (по условию),
(по условию), 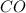 - общая сторона.
- общая сторона.
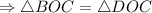 (по I признаку равенства треугольников).
(по I признаку равенства треугольников).
========================================
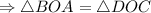 , т.е. мы имеем три равных равнобедренных тр-ка:
, т.е. мы имеем три равных равнобедренных тр-ка:
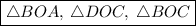
========================================
Рассмотрим 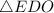 :
:
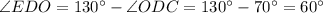 .
.
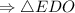 - равносторонний
- равносторонний 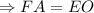
========================================
Рассмотрим геометрическую фигуру 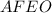 :
:
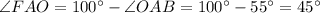 .
.
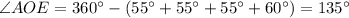 (т.к. в полном угле всего 360°)
(т.к. в полном угле всего 360°)
При пересечении двух параллельных прямых секущей, сумма односторонних углов равна 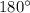 .
.
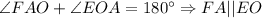
Если у геометрической фигуры есть 4 угла, 4 стороны, а 2 стороны равны и параллельны, то этот четырёхугольник - параллелограмм.
У параллелограмма противоположные углы равны.
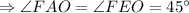 .
.
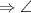 DEF
DEF 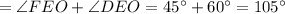
========================================
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Геометрия
-
Інженер будівельного управління Лазаренко 12 лютого 2005 року вчинив прогул, а...
 Варежкамяу22.01.2021 20:27
Варежкамяу22.01.2021 20:27 -
Треугольник ABC- равнобедренный с основанием ВС и m(угол В) = 50°. Определите...
 dfytr8801.07.2022 08:23
dfytr8801.07.2022 08:23 -
В равнобедренном треугольнике ABC с основанием AB на стороне BC взята точка D....
 fatima5208.09.2022 14:27
fatima5208.09.2022 14:27 -
Проведите прямую обозначьте её буквой а и отметьте точки а и в,лежашие на этой...
 yurafeoktistov27.04.2020 00:51
yurafeoktistov27.04.2020 00:51 -
Вокружности проведены диаметр ав и хорда ас. найдите угол сав, если хорда ас стягивает...
 снежана128103.08.2021 11:48
снежана128103.08.2021 11:48 -
Вписанный в окружность угол на 72 градусов меньше соответствующего центрального...
 gghvagsh16703.01.2022 21:03
gghvagsh16703.01.2022 21:03 -
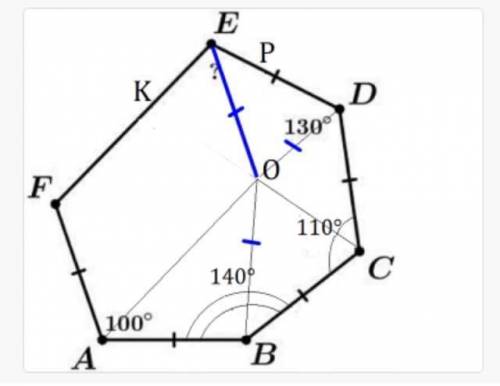
Розгорнутий кут COD поділено променями ON і OK так що кут DON=130°, кут COK=110°....
 yanazyaka22.06.2020 00:38
yanazyaka22.06.2020 00:38 -
Промінь OK ділить COP на два кути. Знайдіть COK, якщо COP дорівнює 120 градусів,...
 Russland200007.12.2020 12:14
Russland200007.12.2020 12:14 -
До іть будь ласка!! Квадрат ABCD. Точка A з координатами (-99;-1) і точка C з...
 kjhf222530.04.2020 09:27
kjhf222530.04.2020 09:27 -
окружность описана около трапеции ABCD , BK высота трапеции , BK = 24 , KD = 32...
 polinafaber26.08.2021 16:12
polinafaber26.08.2021 16:12

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
