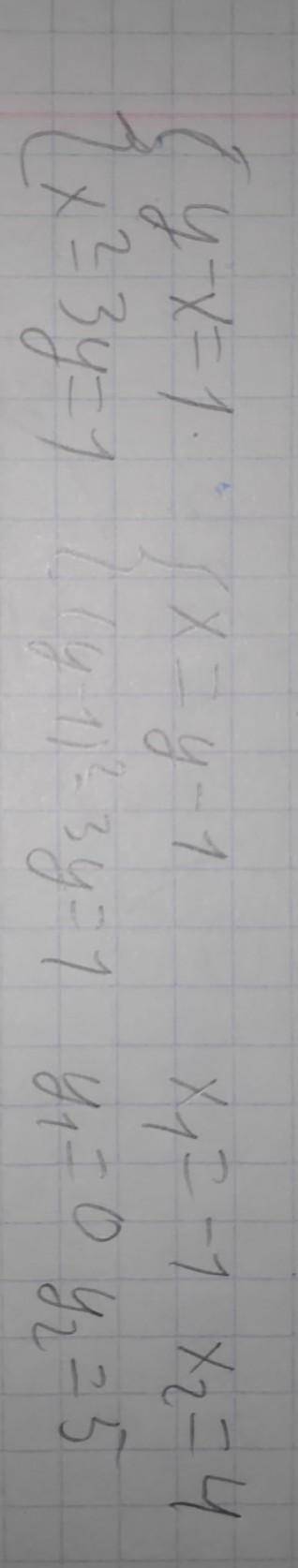Вδabc медианы пересекаются в точке m. прямая pm пересекает сторону ab в точке k, сторону ac в точке l, а точка p лежит на продолжении стороны bc за точку c. докажите, что 1/mk = 1/ml + 1/mp. мелькала тут 8-9 месяцев назад, но её никто так и не решил. примечание: использовать теорему чевы и менелая.

149

179

Посмотреть ответы 2

Ответы на вопрос:

123291Duck

Геометрия

4,6(98 оценок)

Положим что z середина стороны bc . 1)тогда по теореме менелая для треугольника pzm секущая ac получаем cz/pc*pl/ml*am/az=1 , но az медиана , значит am/az=3/2, откуда pl=3ml*pc/(2cz) , значит pm=pl+ml=ml*(3pc+2cz)/(2cz) (*1) 2)по теореме менелая для треугольника bkp секущая az получаем bz/pz*pm/mk*ak/ab=1 либо , что тоже самое что cz/(pc+cz) * pm/mk * ak/ab = 1 откуда mk=pm*(cz/(pc+cz))*(ak/ab) (*2) выразим соотношение ak/ab через pc и cz . 3) по той же теореме для треугольника abc , секущая pk получаем bk/ak * (al/cl) * (pc/(pc+2cz)) = 1 . но (1/2)*(al/cl)*pc/(pc+cz)=1 (теорема менелая для треугольника acz) откуда al/cl=2(pc+cz)/pc . значит bk/ak=(pc+2cz)/(2pc+2cz) , откуда ak/ab=2(pc+cz)/(3pc+4cz) . 4) подставляя (*2) получаем mk=ml(3pc+2cz)/(3pc+4cz) (*3) 5) из (*1) а именно pm=ml*(3pc+2cz)/(2cz) по условию требуется доказать что 1/ml+1/mp=1/mk подставим 1/ml+2cz/(ml*(3pc+2cz)) = (3pc+4cz)/(ml*(3pc+2cz))= 1/mk откуда mk=ml(3pc+2cz)/(3pc+4cz) а это и есть (*3) доказанная ранее.

karpova79

Геометрия

4,7(57 оценок)

ответ во вложении, будут вопросы - обращайтесь.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.