Через середину к медианы вм треугольника авс и вершину а проведена прямая, пересекаюшая сторону вс в точке р. найдите отношение площади треугольника вкр к площади треугольника амк. объясните!

188

498

Посмотреть ответы 2

Ответы на вопрос:

daa86

Геометрия

4,7(10 оценок)

первое, что надо сделать - найти отношение вр/ср; есть много способов, я применяю тот, который используется при доказательстве теоремы чевы. через вершину в проводится прямая ii ас. ар продолжается за точку р до пересечения с этой прямой в точке е.

итак, ве ii ac;

треугольники евк и акм подобны (у них углы равны), поэтому ев/ам = вк/км; в даном случае вк/км = 1, и ев = ам; (то есть эти треугольники просто равны).

отсюда ев = ас/2; (вм - медиана)треугольники евр и аср тоже подобны по тому же признаку, поэтому вр/ср = ев/ас = 1/2; итак, ср = вс*2/3; и, соответственно, площадь треугольника асрsacp = s*2/3; (s - площадь треугольника авс).поскольку площадь треугольника вам равна половине площади авс, а площадь акм равна половине авм, то

sakm = s/4; таким образом, площадь четырехугольника крсм равнаskpcm = sacp - sakm = s*(2/3 - 1/4) = s*5/12; ответ 12/5;

DarkneSS341

Геометрия

4,5(68 оценок)

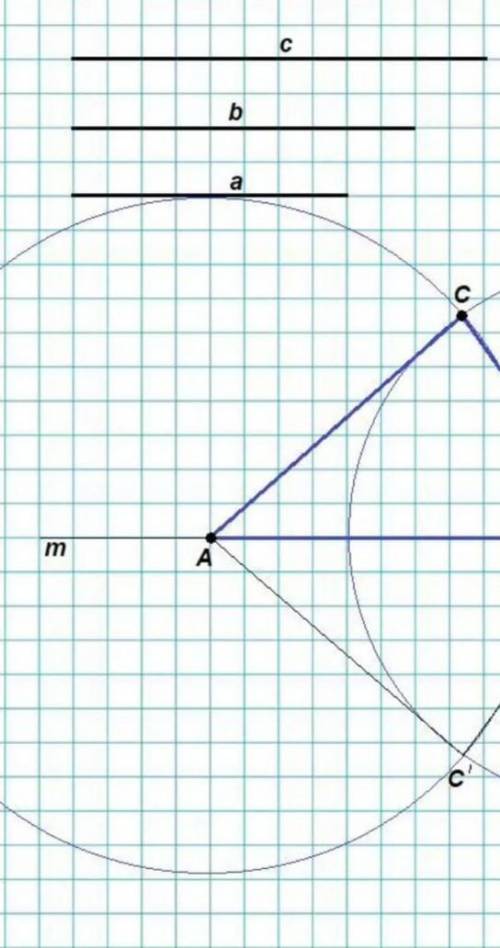
1. На прямой m отложим отрезок АВ = с.

2. Построим окружность с центром в точке А и радиусом, равным b.

3. Построим окружность с центром в точке В и радиусом, равным а.

Одну из точек пересечения окружностей назовем С.

4. Соединим точки А, В и С.

ΔАВС - искомый.

Задача имеет решение, так как с < a + b.

Задача имеет единственное решение, так как ΔABC' = ΔАВС по трем сторонам.

Объяснение:

если не правильно сорян

5. Постройте треугольник АВС по трем сторонам: a = 6 см, b = 5 см, с=4 см

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.