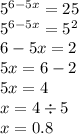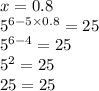Через середину k медианы bm треугольника авс и вершину a проведена прямая, пересекающая сторону вс в точке p. найдите отношение полощади треугольника bkp к площади треугольника amk.

294

455

Посмотреть ответы 2

Ответы на вопрос:

artyomortega

Алгебра

4,5(23 оценок)

первое, что надо сделать - найти отношение вр/ср;

есть много способов, я применяю тот, который используется при доказательстве теоремы чевы. через вершину в проводится прямая ii ас. ар продолжается за точку р до пересечения с этой прямой в точке е.

итак, ве ii ac;

треугольники евк и акм подобны (у них углы равны), поэтому ев/ам = вк/км; в даном случае вк/км = 1, и ев = ам; (то есть эти треугольники просто равны).

отсюда ев = ас/2; (вм - медиана)

треугольники евр и аср тоже подобны по тому же признаку, поэтому вр/ср = ев/ас = 1/2;

итак, ср = вс*2/3; и, соответственно, площадь треугольника аср

sacp = s*2/3; (s - площадь треугольника авс).

поскольку площадь треугольника вам равна половине площади авс, а площадь акм равна половине авм, то

sakm = s/4;

таким образом, площадь четырехугольника крсм равна

skpcm = sacp - sakm = s*(2/3 - 1/4) = s*5/12;

ответ 12/5;

я намеренно не объясняю, почему из того, что ср = вс*2/3; следует, что sacp = s*2/3;

и там я еще два раза использовал тот же прием при вычислении sakm.

конечно, если высоты треугольников равны, их площади относятся, как стороны, к которым эти высоты проведены. я тут это раз 100 уже объяснял, и потом - если постоянно это все расписывать - каждое решение разбухнет до размеров учебника по .

Yana6hhhh

Алгебра

4,4(80 оценок)

${5}^{6 - 5x} = 25 \\ {5}^{6 - 5x} = {5}^{2} \\ 6 - 5x = 2 \\ 5x = 6 - 2 \\ 5x = 4 \\ x = 4 \div 5 \\ x = 0.8$

Проверка:

$x = 0.8 \\ {5}^{6 - 5 \times 0.8} = 25 \\ {5}^{6 - 4} = 25 \\ {5}^{2} = 25 \\ 25 = 25$

верно.

ответ: 0,8

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.