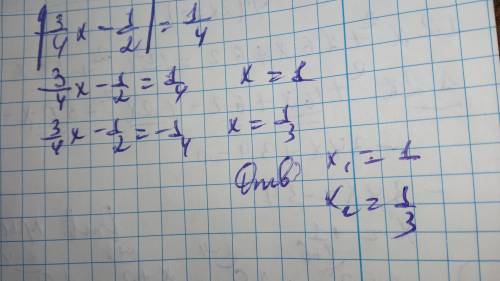Ответы на вопрос:
n=1: 1 = (1(1+1)/2)^2 = (1*2/2)^2=1^2=1 => для n=1 - верноn=k: 1^3+2^3++k^3=(k(k+1)/2)^2 - для kn=k+1: 1^3+2^3++(k+1)^3 = ((k+1)(k+2)/2)^2 - для k+1вернемся к n=k, прибавим к нему соответствующее значение (k+1), то есть (k+1)^31^3+2^3++k^3+(k+1)^3 = (k(k+1)/2)^2 + (k+1)^3 = k^2*(k+1)^2/4 + (k+1)^3 = (k+1)^2 * (k^2/4 + (k+1)) = (k+1)^2/4 (k ^2+ 4k + 4) = (k+1)^2/4*(k+2)^2 = ((k+1)(k+2)/2)^2 - теперь сравните полученный результат с n=k+1. так как они равны, то по методу индукции исходное выражение верно при любом значении n, что и требовалось доказать
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
По заданному значению функции найдите значения остальных тригонометрических...
 shishovtopking07.03.2023 14:54
shishovtopking07.03.2023 14:54 -
(2+sin альфа )(2-sin альфа) + (2+cos альфа) (2-cos альфа)...
 ichmaelz27.11.2021 19:37
ichmaelz27.11.2021 19:37 -
1.) 8 в 9 степени • 4 в 5 степени. 2.) 32 • 16 в 6 степени • 64...
 rrrrrrrrrrrrrrrrt14.02.2023 01:57
rrrrrrrrrrrrrrrrt14.02.2023 01:57 -
Площадь прямоугольного треугольника 96 см^2, а разность его катетов...
 MrZheka1702.03.2022 08:12
MrZheka1702.03.2022 08:12 -
Запишите десятичную дробь ,равную сумме: 5×10^-2+6×10^-3+1×10^-4...
 Soniasizova29.10.2021 06:37
Soniasizova29.10.2021 06:37 -
1разложите на множители: а) (5−а)3 б)(2в+3)3 в)23+с3 г) а3−53 2...
 dfgdfh206.09.2021 09:57
dfgdfh206.09.2021 09:57 -
Найти площадь фигуры, ограниченной линиями y=2^x-1; y=0; x=-3...
 франческа03318.12.2021 22:11
франческа03318.12.2021 22:11 -
Если(a7 =0; 3sin 2x-cosx); (+x^2)^3/2) как написать эту формулу...
 Trap00ra09.09.2021 17:22
Trap00ra09.09.2021 17:22 -
Найдите область определения: y=5/^×2-4...
 polina116523.04.2023 01:21
polina116523.04.2023 01:21 -
Какие отмечены номера 4,5,! заранее ! ...
 mog6907.08.2021 02:09
mog6907.08.2021 02:09

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.