Втрапеции авсд с основаниями ад и вс диагонали пересекаются в точке о, причем ао=3ос.площадь треугольника aoд равна 36.найдите площадь трапеции

149

474

Посмотреть ответы 2

Ответы на вопрос:

kblaginin6gmailm

Геометрия

4,6(38 оценок)

диагонали трапеции «высекают» в ней подобные треугольники. ∆вос~∆ аод по равным углам: углы при основаниях равны как накрестлежащие; при точке о - как вертикальные. k=ао: ос=3. отношение площадей подобных фигур равно квадрату коэффициента их подобия. ⇒ ѕ(аод): ѕ(вос)=3²=9 ⇒ ѕ(аод)=36•9=324.

высота в ∆ аво и вос общая. отношение площадей треугольников с равными высотами равно отношению сторон, к которым высоты проведены. ѕ(аво)=3ѕ(всо)=36•3)=108 аналогично ѕ(сод)=3ѕ(вос)=108. (попутно заметим, что площади треугольников, образованных частями диагоналей и боковыми сторонами трапеции всегда равны именно по этому свойству). площадь трапеции авсд равна сумме площадей четырех треугольников. s(авсд)=36+324+2•108=576 ( ед. площади)

ilyajdbda

Геометрия

4,5(19 оценок)

Самое простое доказательство:

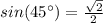$sin(45^\circ) = \frac{\sqrt{2} }{2}$ (табличное значение)

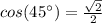$cos(45^\circ) = \frac{\sqrt{2} }{2}$ (табличное значение)

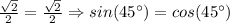
$\frac{\sqrt{2} }{2} = \frac{\sqrt{2} }{2} \Rightarrow sin(45^\circ) = cos(45^\circ)$

Нормально геометрическое доказательство:

См. Рисунок.

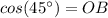
Согласно определению $sin(45^\circ) = OC$ , a $cos(45^\circ) = OB$

В ΔOAB ∠OAB = 180° - 90° = 45°, значит ΔOAB - равнобедренный с основанием OA.

В ΔOAC ∠OAC = 180° - 90° = 45°, значит ΔOAC - равнобедренный с основанием OA.

ΔOAB = ΔOAC по стороне и двум углам. (OA - общая).

Следовательно OC = OB

Значит 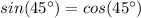$sin(45^\circ) = cos(45^\circ)$

============

Не забывайте нажать " ", поставить оценку и, если ответ удовлетворил, то выберите его как "Лучший"

Успехов в учебе

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.