На окружности по разные стороны от диаметра ab взяты точки m и n. известно, что угол nba = 5°. найдите угол nmb. ответ дайте в градусах , из гиа, мож кто

253

341

Посмотреть ответы 2

Ответы на вопрос:

lizawera

Геометрия

4,5(83 оценок)

Треугольник авn - прямоугольный. угол anb опирается на диаметр ав и потому равен 90° сумма острых углов прямоугольного треугольника 90°. угол nba равен 5° по условию, значит угол nab равен 90°-5°=85° угол nmb равен углу nab как углы опирающиеся на одну и ту же дугу nb. ответ. 85°

astrafikal

Геометрия

4,6(85 оценок)

Единичная полуокружность задается уравнением 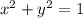x^2+y^2=1 при

условии 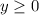$y\geq 0$ .

Вторая и третья точки сразу видно, что не подходят, так как у них ординаты меньше 0 .

Проверим остальные точки . Для этого подставим их координаты в уравнение полуокружности и проверим, выполняется ли равенство .

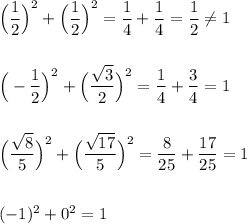
$\Big(\dfrac{1}{2}\Big)^2+\Big(\dfrac{1}{2}\Big)^2=\dfrac{1}{4}+\dfrac{1}{4}=\dfrac{1}{2}\ne 1Big(-\dfrac{1}{2}\Big)^2+\Big(\dfrac{\sqrt3}{2}\Big)^2=\dfrac{1}{4}+\dfrac{3}{4}=1Big(\dfrac{\sqrt8}{5}\Big)^2+\Big(\dfrac{\sqrt{17}}{5}\Big)^2=\dfrac{8}{25}+\dfrac{17}{25}=1(-1)^2+0^2=1$

Единичной полуокружности при условии 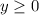$y\geq 0$ принадлежат точки

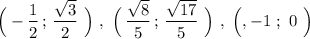
$\Big(-\dfrac{1}{2}\, ;\, \dfrac{\sqrt3}{2}\ \Big)\ ,\ \Big(\, \dfrac{\sqrt8}{5}\, ;\, \dfrac{\sqrt{17}}{5}\ \Big)\ ,\ \Big(, -1\ ;\ 0\ \Big)$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.