Hjk345

21.09.2022 07:49

Математика

Есть ответ 👍

Делитель увеличили в 12 раз. что нужно сделать с делимым, чтобы частное увеличилось в 60 раз? а) уменьшить в 5 раз б) уменьшить в 720 раз в) увеличить в 5 раз г) увеличить в 720 раз

290

360

Посмотреть ответы 2

Ответы на вопрос:

mrtwice

Математика

4,6(90 оценок)

Пусть а - делитель, в - делимое, с- частное. с = а/в 60с = / 12в верное равенство получается, если 60с = 720а/12в ответ г) делимое нужно увеличить в 720 раз

Viktor2017Kot

Математика

4,4(68 оценок)

78-я задача: 35; 79-я задача: 21.

Пошаговое объяснение:

Сделаем заодно и 78-ю задачу. Поскольку x≠0⇒x²+11x-6=0; x²+11x=6. Поэтому

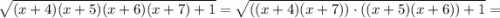
$\sqrt{(x+4)(x+5)(x+6)(x+7)+1}=\sqrt{\left((x+4)(x+7)\right)\cdot\left((x+5)(x+6)\right)+1}=$

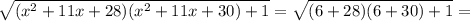
$\sqrt{(x^2+11x+28)(x^2+11x+30)+1}=\sqrt{(6+28)(6+30)+1}=$

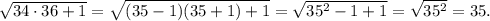
$\sqrt{34\cdot 36+1}=\sqrt{(35-1)(35+1)+1}=\sqrt{35^2-1+1}=\sqrt{35^2}=35.$

Переходим к 79-й задаче. Упростим задачу, сделав замену x-1=a, y-1=b, z-1=c. Для a, b, c задача свелась к подсчету числа неотрицательных целых троек таких, что a+b+c=16-3=13. Обозначим через 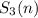S_3(n) количество троек неотрицательных целых чисел, чья сумма равна n.

Обозначими через 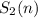S_2(n) количество двоек неотрицательных целых чисел, чья сумма равна n. Это количество подсчитать совсем просто.

Если n=2k, то есть n - четное число, то двойки имеют вид (0;2k);

(1;2k-1); (2;2k-2);...; (k;k) - их k+1 штука, то есть 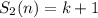S_2(n)=k+1 .

Если n=2k+1, то двойки имеют вид (0;2k+1); (1;2k); (2;2k-1);... ; (k;k+1) - их

k+1 штука, то есть 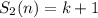S_2(n)=k+1 .

Для знающих, что такое целая часть [n] числа n, получаем для 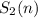S_2(n) такую формулу:

$S_2(n)=\left[\dfrac{n}{2}\right]+1.$

(Целая часть числа n - это наибольшее целое число, не большее n.)

Мы подготовили почву для получения рекуррентной формулы. Разобьем все тройки на тройки, включающие в себя хотя бы один ноль, и тройки без нулей.

Разберемся с тройками первого типа. Уберем из таких троек одно число, а именно ноль. Тройка станет двойкой с прежней суммой, поэтому таких троек 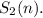S_2(n).

Переходим к тройкам без нулей, то есть к тройкам из натуральных чисел. Вычитая из каждого из них 1, получаем тройки из неотрицательных чисел, чья сумма равна n-3 - таких троек в наших обозначениях 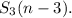S_3(n-3).

Отсюда следует формула

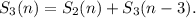
S_3(n)=S_2(n)+S_3(n-3).

Иными словами,

$S_3(n)=\left[\dfrac{n}{2}\right]+1+S_3(n-3).$

Применяя эту формулу, получаем:

$S_3(13)=\left[\dfrac{13}{2}\right]+1+S_3(10)=7+\left[\dfrac{10}{2}\right]+1+S_3(7)=$

$13+\left[\dfrac{7}{2}\right]+1+S_3(4)=17+\left[\dfrac{4}{2}\right]+1+S_3(1)=20+1=21.$

Замечание. Возможно, кому-то решение покажется слишком сложным - ведь быстрее просто выписать все тройки. Тогда мой подсказывает, как можно организовать прямой подсчет. Во-первых, можно отказаться от перехода от натуральных чисел к целым неотрицательным. Тогда все тройки разбиваем на те, в которых есть хотя бы одна 1 - это (1;1;14); (1;2;13); (1;3;12); (1;4;11); (1;5;10);

(1;6;9); (1;7;8) - здесь 7 троек, а остальные (они уже без единой единицы) разбиваем на те, в которых есть хотя бы одна двойка - это

(2;2;12); (2;3;11); (2;4;10); (2;5;9); (2;6;8); (2;7;7) - здесь 6 троек, а остальные (они уже без единиц и двоек) разбиваем на те, в которых есть хотя бы одна тройка - это (3;3;10); (3;4;9); (3;5;8); (3;6;7) - здесь 4 тройки, а остальные (они уже без единиц, двоек и троек) разбиваем на те, в которых есть хотя бы одна четверка - это (4;4;8); (4;5;7); (4;6;6) - здесь 3 тройки, а остальные (они уже без единиц, двоек, троек и четверок) разбиваем на те, в которых есть хотя бы одна пятерка - это (5;5;6) - здесь 1 тройка, а остальные (они уже без единиц, двоек, троек, четверок и пятерок) - ау! а где вы, остальные? - нет их!

Поэтому всего 7+6+4+3+1=21 тройка.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.