Регистрация Спросить otvet5GPT
Dashatatur1
24.01.2022 02:57
Геометрия
Есть ответ 👍

1. сторона равностороннего треугольника равна 14корень3 см. найдите биссектрису этого треугольника. 2. в треугольнике abc ab=10 см, bc=17 см, ac=21 см. найдите высоту bd.

226
264
Посмотреть ответы 2

Ответы на вопрос:

69supreme
69supreme
4,6(84 оценок)

1) (14sqrt(3))^2-(7sqrt(3))^2=588-147=441

bissektrisa= sqrt(441)=21

2) p=a+b+c/2=10+17+21=48/2=24

s=sqrt(24*(24-10)(24-17)(24-21))=84

s=1/2*ac*h

84=1/2*21*h

h=8

daniabloger
daniabloger
4,8(30 оценок)

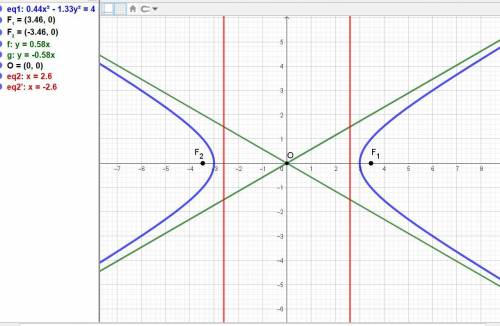
определить каноническое уравнение гиперболы, если угол между асимптотами равен 60 градусов и С= 2 корня из 3.

Угол между асимптотой и осью Ох равен 60/2 = 30 градусов.

Угловой её коэффициент или тангенс угла наклона к оси Ох равен

1/√3. Значит, в уравнениях асимптот у = +-(b/a)x значение b/a = 1/√3.

Отсюда находим соотношение a = b√3.

Далее используем заданное значение с = 2√3.

Так как с² = a² + b², то используем найденное соотношение a и b .

(2√3)² = (b√3)² + b²,

12 = 3b² + b²,

12 = 4b²,

b² = 12/4 = 3,

b = √3.

Тогда а = b√3 = √3*√3 = 3.

Найдены параметры a и b канонического уравнения параболы:

(x²/a²) - (y²/b²) = 1.

Подставляем найденные параметры и получаем

ответ: (x²/3²) - (y²/(√3)²) = 1.

Эксцентриситет гиперболы равен е = с/а = 2√3/3.

Уравнения асимптот у = +-(√3/3)x.

Координаты фокусов F1,F2 = (+-2√3; 0).

Уравнения директрис х = +-a²/c = +-3√3/2.


определить каноническое уравнение гиперболы, если угол между асимптотами равен 60 градусов и С= 2 ко

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS