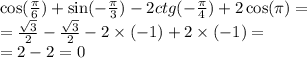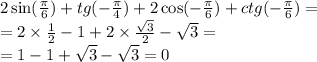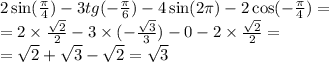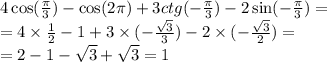Как найти угол 4 если 1 = 60°, 2 = 120°, 3 = 53° а 4 и 3 накрест лежащие
189
266
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
15а(p-q) 20b(p-q) 8 класс надо(это дробь)...
 Akimneznaet12318.03.2020 04:28
Akimneznaet12318.03.2020 04:28 -
Найдите допустимые значения переменной в выражении а) (n+3): (n во 2 степени -2n)...
 galinaegi230.10.2021 21:05
galinaegi230.10.2021 21:05 -
Решить уравнение 1+5++х=630, где х— натуральное число...
 znanija11426.01.2023 19:51
znanija11426.01.2023 19:51 -
Разложить на множители. проблема в том, что я забыл, что делать, когда в подобной...
 Ксюша1009200714.07.2020 10:47
Ксюша1009200714.07.2020 10:47 -
Решите уравнение (6х-1)(6х+1)-4х(9х+2)=1 и еще один пример х-3х(1-12х)=11-(5-6х)(6х+5)...
 red01102.12.2021 06:07
red01102.12.2021 06:07 -
Перечислить свойства функции y=2x-1,и построить график этой функции...
 nomakade08.10.2020 05:42
nomakade08.10.2020 05:42 -
К1 вариант 14 найти значение выражения 21p+6q при p=1/7,q=-1/12....
 andriytustanov12.12.2020 03:44
andriytustanov12.12.2020 03:44 -
Увеличели на треть и получили 120. найдите исходное число а)90 б)120 1/3 в)80...
 aminka009518.01.2021 10:34
aminka009518.01.2021 10:34 -
Решить формула сокращённого умножения...
 hjhytu18.07.2022 15:20
hjhytu18.07.2022 15:20 -
(-1/3)^4×(-1/3)^8= можно с обеснением...
 Енотик8305.05.2022 06:55
Енотик8305.05.2022 06:55

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.