15.07.2020 15:53

Есть ответ 👍

Сторона основания правильной четырехугольной призмы равна 5см,а высота 9см.вычислите площадь боковой и полной поверхности призмы

293

303

Посмотреть ответы 2

Ответы на вопрос:

ksapko

Геометрия

4,5(17 оценок)

Площадь боковой поверхности= 5*9*4=180 площадь полной вредности призмы= боковая+ основание=180+5*5=205

ZA25

Геометрия

4,7(87 оценок)

а) боковая сторона равна 4√3 см;

б) медиана, проведённая к основанию, равна 2√3 см;

в) медиана, проведённая к боковой стороне, равна 2√21 см.

Объяснение:

Дано:

ΔАВС:

АВ = ВС - боковые стороны

АС = 12 см - основание

∠А = ∠С = 30° - углы при основании

Найти:

а) АВ - боковую сторону

б) ВМ - медиану, проведённую к основанию

в) АК - медиану, проведённую к боковой стороне

а)

В равнобедренном треугольнике медиана, проведённая к основанию, делит основание пополам, то есть

АМ = СМ =0,5АС = 6 см;

и является высотой, поэтому ΔАВМ - прямоугольный с углом

∠ВМА = 90°.

Тогда

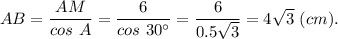
$AB = \dfrac{AM}{cos~A} = \dfrac{6}{cos~30^{\circ}} = \dfrac{6}{0.5\sqrt{3}} = 4\sqrt{3} ~(cm).$

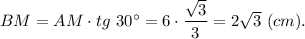
$BM = AM\cdot tg~30^{\circ} = 6\cdot \dfrac{\sqrt{3} }{3} = 2\sqrt{3} ~(cm).$

в)

В ΔАВС: ∠В = 180° - 2 · 30° = 120°

Рассмотрим ΔАВК.

АВ = 4√3 см; ВК = 0,5 ВС = 2√3 см; ∠В = 120°.

По теореме косинусов найдём ВК

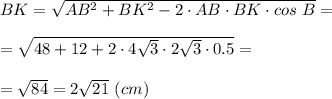
$BK = \sqrt{AB^2 + BK^2 - 2\cdot AB\cdot BK\cdot cos~B} =\\ \\ = \sqrt{48 + 12 + 2\cdot 4\sqrt{3} \cdot 2\sqrt{3} \cdot 0.5} =\\ \\ = \sqrt{84} =2\sqrt{21} ~(cm)$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.