Углы при одном из оснований трапеции равны 50 и 40 а отрезки соединяющие середины противоположных сторон трапеции равны 15 и 13 найдите основания трапеции.

281

489

Посмотреть ответы 2

Ответы на вопрос:

KatyaBelchik12

Геометрия

4,7(11 оценок)

Сделаем рисунок трапеции авсд. так как углы при основании аd в сумме равны 50°+40°=90°, продолжения сторон ав и сd пересекаются в точке о под прямым углом ( третий угол образовавшегося треугольника аоd=180°-90°=90°) по условию нм=13см, ке=15см проведем вт праллельно оd. угол авт - прямой. треугольник авт - прямоугольный. прямоугольные треугольники аоd и авт подобны по прямому углу и острому углу а, общему для обоих треугольников. медиана вр треугольника авт параллельна ом и, следовательно, параллельна нм и равна ей. вр=нм=13см медиана прямоугольного треугольника равна половине его гипотенузы. ат=2 вр=26см кф - средняя линия треугольника авт и равна ат: 2=26: 2=13cм рассмотрим четырехугольник всdт. это параллелограмм по построению. вс=еf еf=ке-кф=15-13=2cм вс=fе=тd=2см ад=ат+тд=26+2=28см ответ: основания трапеции равны 2см и 28см. решение может быть неверным, сама не любительница .^_^

McBlanse

Геометрия

4,7(91 оценок)

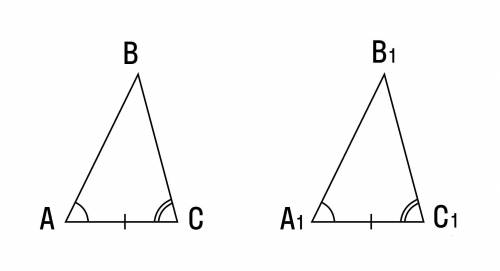
Возьмём 2 треугольника

Нужно доказать, что △ABC = △A1B1C1.

Доказательство:

Путем наложения △ABC на △A1B1C1, совмещаем вершину А с вершиной A1, вершины В и В1 лежат по одну сторону от А1С1.

АС совмещается с A1C1, вершина C совпадает с C1

AB накладывается на A1B1

CB накладывается на C1B1

Вершина B совпадает с вершиной B1.

Если Всё совмещается => △ABC совмещается с △A1B1C1, значит, △ABC = △A1B1C1 .

по другому не докажешь)

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.