Регистрация Спросить otvet5GPT
илья20067
13.03.2020 02:20
Математика
Есть ответ 👍

1)2x^2+2x+1=02)x^4+x^2-4=0 3)3x^2+18x+9=0 4)x^8+x^4-2=0 5)x16+x8+10=0 6)2x^*-8=0 7)10x^8-1000=0 8)10x^4=10 9)8x^2+6x-10=0 10)3x+2=3x+2

118
166
Посмотреть ответы 2

Ответы на вопрос:

sofia042
sofia042
4,5(48 оценок)
1)  2x^2+2x+1=0 d=b^2-4*a*c=4-8=-4нет корней.2) x^4+x^2-4=0x^2(x^2+1)-4=0(x^2-4)(x^2+1)=0x^2=+-2; 3)3x^2+18x+9=0d=324-108=216x=(-b+-√d)/2a x(1)=(-18+6√6 )/6=(6(√6-3 ))/6=√6-3 x(2)=-//-=√6+3 как то так, можешь по моим примерам порешать дальше, уж слишком их много, и я уже не соображаю
никита2005216665
никита2005216665
4,8(74 оценок)

ответ: 8π

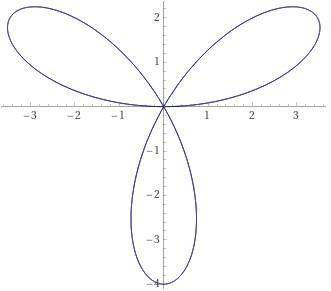
Пошаговое объяснение: r=4sin (3ф) это уравнение 3-х лепестковой розы в полярной системе координат.

Максимальное значение r=4, min r=0.  

Период функции Sin (3ф)= 2π/3 Разделим на3 равные части лучами [0; 2π]  в полярной системе координат, выполним рисунок (прилагается). Найдём площадь S₁ половины лепестка розы, а затем умножим на 6. Пределы интегрирования от 0 до π/6 ( у знака интеграла плохо видно)

S₁= 1/2·∫₀ⁿ⁾⁶(4sin(3ф))²dф= 1/2·∫₀ⁿ⁾⁶ 16sin²(3ф)dф=8·∫₀ⁿ⁾⁶sin²(3ф)dф=  

4·∫₀ⁿ⁾⁶(1-сos(6ф)dф= 4·∫₀ⁿ⁾⁶dф  - 4/6 ·∫₀ⁿ⁾⁶сos(6ф)d(6ф)=

=(4ф-sin(6ф))|₀ⁿ⁽⁶=2π/3 - sin(π)-0+0=2π/3  

Значит S=6·S₁=6·(2π/3)=8π


Вычислить площадь фигуры ограниченной трехлепестковой розой ρ=4sin3φ

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS