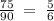Регистрация Спросить otvet5GPT
Йфяалмглиоаиопр
02.03.2021 15:48
Математика
Есть ответ 👍

Найти общее решение дифференциального уравнения x*y'-4y=x^2*y^1/2

179
404
Посмотреть ответы 2

Ответы на вопрос:

Tata123N
Tata123N
4,6(21 оценок)
Xy' - 4y = x²*√y (xy' - 4y): 2x√y = (x²√y): 2x√y    разделим обе части на 2x√y y'/(2√y)  -  (2√y)/x = x/2   (1) u = √y    заменим √y на u u' = (√y)' = (y'/2)(y^(-1/2)) = y'/(2√y)  найдём производную от  u y'/(2√y) = u' заменим в уравнении  (1)   y'/(2√y) на u' , а  √y на u: u' - (2u)/x = x/2 (u' - (2u)/x): x² = (x/2): x²  разделим обе части на x² u'/x² - 2u/x³ = 1/2x u'(1/x²) - u(2/x³ )= 1/2x  (2) заметим, что -(2/x³ ) = (1/x²)', проверим: (1/x²)' = (x^-2)' = -2(x^-3) = -2/x³ заменим в уравнении  (2)   -2/x³  на (1/x²)' u'(1/x²) + u(1/x²)' = 1/2x производная произведения функций: (f*g)' = f ' * g     +  f * g'    f = u; g = 1/x²  (f*g) = 1/2x 1/2x = u'(1/x²) + u(1/x²)' (u(1/x²))' = 1/2x (u/x²)' = 1/2x интегрируем обе части по dx ∫(u/x²)'dx = (ʃ dx/x)/2    ∫(u/x²)'dx = u/x²        ∫dx/x = ln(x)/2 + c u/x² =  ln(x)/2 + c  ( c - константа) u = ( ln(x)/2 + c)*x² u = √y найдём у y = u² = (( ln(x)/2 + c)*x²)²  = (x^4)( ln(x)/2 + c)² результат: y  =  (x^4)*( ln(x)/2 + c)²  при желании можно раскрыть скобки)
сакина12
сакина12
4,8(8 оценок)

\frac{75}{90} \: = \: \frac{5}{6}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS