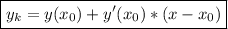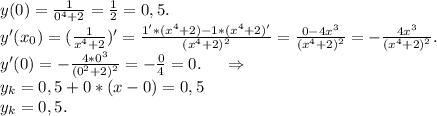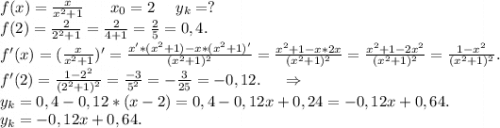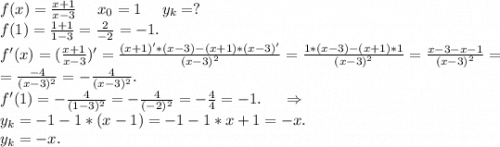Ответы на вопрос:
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Алгебра
-
Площадь квадрата равна 8 см2. Найдите диагональ квадрата ...
 mane200911.05.2020 03:54
mane200911.05.2020 03:54 -
НАДО составить уравнение касательной и нормами к параболе y=-x²+7x+3 в...
 atom3322.08.2022 11:13
atom3322.08.2022 11:13 -
Чому дорівнює кут A трикутника...
 филя2417.01.2021 17:01
филя2417.01.2021 17:01 -
Привет соч по алгебре можете я новенький дам 20 больше нет...
 Chchcjcujcj16.02.2022 16:57
Chchcjcujcj16.02.2022 16:57 -
Найдите точку минимума функции у=х^3-13х^2-9х+2 ...
 imuraveva20.11.2022 16:22
imuraveva20.11.2022 16:22 -
Дана арифметическая прогрессия 2; 5; 8; 11; найдите разность данной арифметической...
 tan197801.10.2022 04:33
tan197801.10.2022 04:33 -
Найдите частное 3,6*10 в -7 степени/0.3*10 в -6 степени. ответ запишите...
 uglyfrosha15.04.2021 06:36
uglyfrosha15.04.2021 06:36 -
Известно,что sin α + cos α= найти sin³ α + cos³ α напишите подробно :...
 Алёнатян11120.03.2021 05:25
Алёнатян11120.03.2021 05:25 -
Вкиоске воздушные шарики четырех цветов. сколько существует вариантов...
 tatanapahomova917.02.2020 09:44
tatanapahomova917.02.2020 09:44 -
При каких p система имеет решения 5x+2≥17+2x p+2x≤3+x...
 mkmoonlightovwm0o10.02.2020 02:16
mkmoonlightovwm0o10.02.2020 02:16

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.