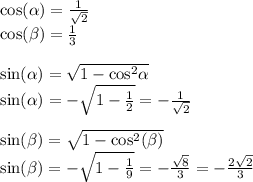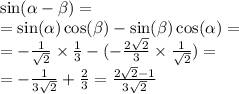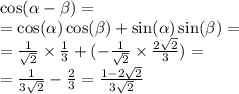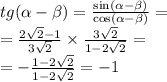Регистрация Спросить otvet5GPT
Sashalizanika
22.12.2022 12:14
Алгебра
Есть ответ 👍

Область определения функций y=2x-4/x^2+9 и y=под корнем 3x-x^2 распишите

214
340
Посмотреть ответы 2

Ответы на вопрос:

Ананасик20031
Ананасик20031
4,7(79 оценок)

у=под корнем 3x-x^2> =0 потому что подкоренное выражение всегда неотрицательно.

решаем методом интервалов получаем:

-x^2+3x> =0 (*-1)( умножаем на минус один и знак меняем)

x^2-3x< =0               x(x-3)=0

                              x=0   x-3=0

    0 =< x< =3                     x=3

а второе будет неравно нулю. так как в знаменателе квадрат числа, а нулем быть это число не должно, так как на ноль делить нельзя.

 

2x-4/x^2≠0

2x(1-2x)≠0

2x≠0   1-2x≠0

x≠0     x≠1/2

 

PaulinaWalters
PaulinaWalters
4,4(6 оценок)

\cos( \alpha ) = \frac{1}{ \sqrt{2} } \\ \cos( \beta ) = \frac{1}{3} \\ \\ \sin( \alpha ) = \sqrt{1 - { \cos }^{2} \alpha } \\ \sin( \alpha ) = - \sqrt{1 - \frac{1}{2} } = - \frac{1}{ \sqrt{2} } \\ \\ \sin( \beta ) = \sqrt{1 - \cos ^{2} ( \beta ) } \\ \sin( \beta ) = - \sqrt{1 - \frac{1}{9} } = - \frac{ \sqrt{8} }{3} = - \frac{2 \sqrt{2} }{3}

1

\sin( \alpha - \beta ) = \\ = \sin( \alpha ) \cos( \beta ) - \sin( \beta ) \cos( \alpha ) = \\ = - \frac{1}{ \sqrt{2} } \times \frac{1}{3} - ( - \frac{2 \sqrt{2} }{3} \times \frac{1}{ \sqrt{2} } ) = \\ = - \frac{1}{3 \sqrt{2} } + \frac{2}{3} = \frac{2 \sqrt{2} - 1 }{3 \sqrt{2} }

2

\cos( \alpha - \beta ) = \\ = \cos( \alpha ) \cos( \beta ) + \sin( \alpha ) \sin( \beta ) = \\ = \frac{1}{ \sqrt{2} } \times \frac{1}{3} + ( - \frac{ 1}{ \sqrt{2} } \times \frac{2 \sqrt{2} }{3} ) = \\ = \frac{1}{3 \sqrt{2} } - \frac{2}{3} = \frac{1 - 2 \sqrt{2} }{3 \sqrt{2} }

tg( \alpha - \beta ) = \frac{ \sin( \alpha - \beta ) }{ \cos( \alpha - \beta ) } = \\ = \frac{2 \sqrt{2} - 1 }{3 \sqrt{2} } \times \frac{3 \sqrt{2} }{1 - 2 \sqrt{2} } = \\ = - \frac{1 - 2 \sqrt{2} }{1 - 2 \sqrt{2} } = - 1

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS