Аданы уравнения типа f(x,y)=0: у–3х+ 4=0. у–х2+ 6х–8=0 х2+ у2–16=0 изобразить графики с оответствующих функций и отметить на координатной плоскости решение каждого уравнения

171

413

Посмотреть ответы 2

Ответы на вопрос:

vprivat1604

Математика

4,4(24 оценок)

Первое уравнение задает линейную функцию на плоскости. графиком является прямая, проходящая через точки (0; -4) и (3; 5) второе уравнение задает параболу у=х²-6х+8 ветви параболы направлены вверх, вершина в точке (3; -1) так как х²-6х+8=х²+6х+9-9+8=(х-3)²-1 парабола пересекает ось ох в точках х=2 и х=4, так как х²-6х+8=(х-2)(х-4) третье уравнение окружности х²+у²=4² с центром в точке (0; 0) и радиусом 4

Алшиния

Математика

4,5(29 оценок)

Дано: прямая а, т. М∉а

Доказать: существует единственная прямая b||a, M∈b

Доказательство:

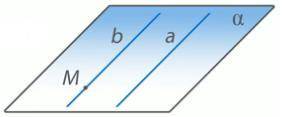
Через прямую а и точку, не лежащую на ней, можно провести единственную плоскость α (Рис.). В плоскости α можно провести единственную прямую b, параллельную а, проходящую через точку M (из аксиомы планиметрии о параллельных прямых). Существование такой прямой доказано.

Докажем единственность такой прямой. Предположим, что существует другая прямая с, проходящая через точку M и параллельная прямой а. Пусть параллельные прямые а и с лежат в плоскости β. Тогда плоскость β проходит через точку M и прямую а. Но через точку M и прямую а проходит единственная плоскость (в силу теоремы 1). Значит, плоскости β и α совпадают. Из аксиомы параллельных прямых, следует, что прямые b и с совпадают, так как в плоскости существует единственная прямая, проходящая через данную точку и параллельная заданной прямой. Единственность доказана.

Я сначала, конечно, подумал воспользоваться теорией неэлементарной школьной геометрии, а аналитической, но так как программа десятого класса не нацелена на глубокое понимание основ взаимного расположения прямых в пространстве, то было решено ограничиться понятным для учащихся среднего общего образования языком:)

10 класс. Теорема о параллельных прямых в пространстве. Мне не . Есть теорема, через любую точку в

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.