Регистрация Спросить otvet5GPT
Аринаqwe
14.03.2020 05:00
Алгебра
Есть ответ 👍

При каких значениях a и b система уравнений имеет бесконечно множество решений?

300
500
Посмотреть ответы 2

Ответы на вопрос:

zadorina66
zadorina66
4,5(5 оценок)
Находим главный определитель системы a  -4,5                 =-3a+9 =0    3a=9  a=3 2  -3 находим определители 6  -4,5                 = -18+4,5b=0  4,5b=18  b=4 b  -3 a  6           = ab-12=0  ab=12  3b=12  b=4 2   b  если определители системы равны 0, то система либо имеет бесконечно много решений либо несовместна. проверим систему при a=3 b=4 3x-4,5y=6 2x-3y=4  умножив второе уравнение на 1,5 получим первое система сводится к уравнению 3х-4,5у=6 которое имеет бесконечное чило решений ответ a=3 b=4
anaStasyaplus
anaStasyaplus
4,5(3 оценок)

Коэффициент одночлена k - это число, стоящее перед буквенной частью в произведении после приведения одночлена к стандартному виду.

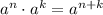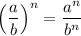Используем формулы:   a^{n}\cdot a^{k}=a^{n+k}  ,  \Big(\dfrac{a}{b}\Big)^{n}=\dfrac{a^{n}}{b^{n}}  .

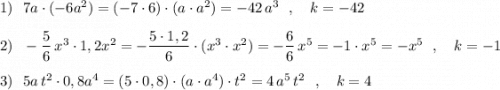
1)\ \ 7a\cdot (-6a^2)=(-7\cdot 6)\cdot (a\cdot a^2)=-42\, a^3\ \ ,\ \ \ k=-422)\ \ -\dfrac{5}{6}\, x^3\cdot 1,2x^2=-\dfrac{5\cdot 1,2}{6}\cdot (x^3\cdot x^2)=-\dfrac{6}{6}\, x^5=-1\cdot x^5=-x^5\ \ ,\ \ \ k=-13)\ \ 5a\, t^2\cdot 0,8a^4=(5\cdot 0,8)\cdot (a\cdot a^4)\cdot t^2=4\, a^5\, t^2\ \ ,\ \ \ k=4

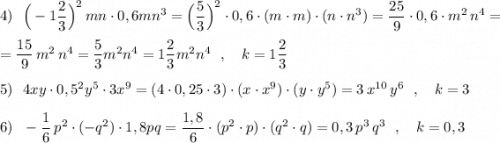
4)\ \ \Big(-1\dfrac{2}{3}\Big)^2\, mn\cdot 0,6mn^3=\Big(\dfrac{5}{3}\Big)^2\cdot 0,6\cdot (m\cdot m)\cdot (n\cdot n^3)=\dfrac{25}{9}\cdot 0,6\cdot m^2\, n^4==\dfrac{15}{9}\, m^2\, n^4=\dfrac{5}{3}m^2n^4=1\dfrac{2}{3}m^2n^4\ \ ,\ \ \ k=1\dfrac{2}{3}5)\ \ 4xy\cdot 0,5^2y^5\cdot 3x^9=(4\cdot 0,25\cdot 3)\cdot (x\cdot x^9)\cdot (y\cdot y^5)=3\, x^{10}\, y^6\ \ ,\ \ \ k=36)\ \ -\dfrac{1}{6}\,p^2\cdot (-q^2)\cdot 1,8pq=\dfrac{1,8}{6}\cdot (p^2\cdot p)\cdot (q^2\cdot q)=0,3\, p^3\, q^3\ \ ,\ \ \ k=0,3

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Алгебра

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS