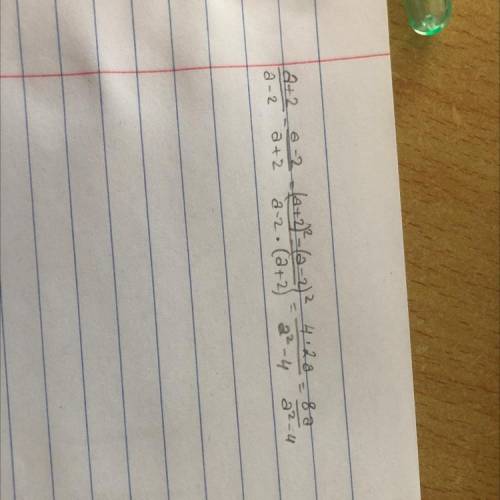Верно ли, что любое положительное рациональное число можно представить как отношение произведения факториалов (не обязательно разных) простых чисел? например

205

436

Посмотреть ответы 2

Ответы на вопрос:

Алексей08032005

Алгебра

4,5(54 оценок)

Верно. покажем, что любое натуральное число n можно представить в указанном виде (а значит, и отношение натуральных чисел будет представимо в таком виде). если n = 1, можно написать, например, n = 2! / 2! по основной теореме арифметики любое натуральное число, большее 1, однозначно (с точностью до порядка сомножителей) представимо в виде произведения простых множителей: (alpha - номер простого числа; все простые числа расположены в порядке возрастания) докажем требуемое утверждение индукцией по alpha_k. база: для alpha_k = 1 утверждение очевидно: первое простое число совпадает со своим факториалом: 2 = 2! переход. пусть для всех alpha_k < m утверждение выполнено. пусть n = q * p^l, причем номер p равен m и q не делится на p. 1) q по предположению представимо в нужном виде. 2) заметим, что p = p! / (p- (p-1)! не содержит простых чисел с номерами, не меньших m, так что по предположению индукции представимо в виде дроби нужного вида. тогда и p! /(p-1)! представимо в нужном виде. 3) остается перемножить дробь для q и l дробей для p. переход доказан.

topcekstrimer

Алгебра

4,7(56 оценок)

Дададададададдааалаадда во
Решите письменно в тетради

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.