Ответы на вопрос:
Пошаговое объяснение:
а) 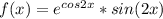
![f'(x) =\left[\begin{array}{ccc}u=2x\\du = 2dx\end{array}\right] = \frac{1}{2}\int\limits sinu *e^{cosu} \, du } =\left[\begin{array}{ccc}s=cosu\\ds = -sinu du\end{array}\right] =](/tpl/images/3768/8873/7fd70.png)
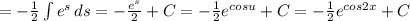
б) 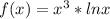
![f'(x) = \left[\begin{array}{ccc}\int\limits{f } \, dg = f*g -\int\limits {g} \, df \\f = lnx ; df = \frac{1}{x} dx\\g = \frac{x^{4} x}{4 } ; dg = x^{3} dx \end{array}\right] = \frac{4}{4}x^{4} lnx - \frac{1}{4} \int\limits x^{3} \, dx = \frac{x^{4} }{4} lnx - \frac{x^{4}}{16} + C](/tpl/images/3768/8873/fb4d5.png)
в) 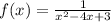
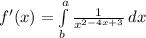
дробь разложим на множители и возьмем интеграл суммы
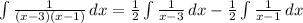
теперь по отдельности посчитаем 1ый и 2ой интегралы (это чтобы не путаться в длинных записях)
![\int\limits {\frac{1}{x-3}} \, dx = \left[\begin{array}{ccc}u=x-3\\du=dx\\\end{array}\right] = \int\limits {\frac{1}{u} } \, du = lnu +C = ln(x-3) + C](/tpl/images/3768/8873/04dc7.png)
![\int\limits {\frac{1}{x-1}} \, dx = \left[\begin{array}{ccc}u=x-1\\du=dx\\\end{array}\right] = \int\limits {\frac{1}{u} } \, du = lnu +C = ln(x-1) + C](/tpl/images/3768/8873/71c62.png)
в результате получим ответ
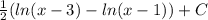
Здесь еще можно применить модуль к аргументу логарифма, чтобы расширить его диапазон его диапазон (ну, это уже как кому нравится)
Реши свою проблему, спроси otvet5GPT
-
Быстро
Мгновенный ответ на твой вопрос -
Точно
Бот обладает знаниями во всех сферах -
Бесплатно
Задай вопрос и получи ответ бесплатно

Популярно: Математика
-
Упристони стояли 2 катера ракета на подводных крыльях и 6 моторных...
 данил1013123.03.2023 06:55
данил1013123.03.2023 06:55 -
Решить 1. одно число больше другого в 4,5 раза. если от большего числа...
 OlyaMonokova29.04.2021 10:05
OlyaMonokova29.04.2021 10:05 -
1. как называется угол, который больше 90°, но меньше 180°? а) острый...
 Влад20061927.04.2022 07:07
Влад20061927.04.2022 07:07 -
Прошу вас, дорогие сверхразумы, решить примеры на данной фотокарточке....
 saaangelina20.02.2023 01:15
saaangelina20.02.2023 01:15 -
Найдите половину квадрата числа а,если 4/7 числа а равны 28...
 neshm08meshca22.04.2020 22:42
neshm08meshca22.04.2020 22:42 -
Функция полезности имеет вид : u(x1,x2) = 4x1x2, а доход выделенный...
 tanyaaksenova122.12.2021 02:34
tanyaaksenova122.12.2021 02:34 -
1сектор с центральным углом 120 градусов составляет круга если круг...
 Your1sad1waifu18.05.2023 16:39
Your1sad1waifu18.05.2023 16:39 -
Перед витязем на распутье 3 дороги, которые он выбирает с вероятностью...
 Danil022008.06.2020 01:23
Danil022008.06.2020 01:23 -
Решение диагностической работы по 8 класс 1 вариант 1 часть модуль...
 kdjdjd1Dndnd06.10.2022 16:52
kdjdjd1Dndnd06.10.2022 16:52 -
Человек изучающий недра земли 6 букв? ?...
 30Космос0304.01.2020 01:02
30Космос0304.01.2020 01:02

Есть вопросы?
-
Как otvet5GPT работает?
otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса. -
Сколько это стоит?
Проект находиться на стадии тестирования и все услуги бесплатны. -
Могу ли я использовать otvet5GPT в школе?
Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое! -
В чем отличия от ChatGPT?
otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
