По стороне основания "а" найти боковую поверхность правильной четырехугольной пирамиды,у которой диагональное сечение равновелико основанию. подробно

227

352

Посмотреть ответы 2

Ответы на вопрос:

kulagindemid20

Геометрия

4,4(84 оценок)

подробно.

площадь основания a^2; диагональ основания a*корень(2). это - основание треугольника, который - диагональное сечение. треугольник этот равнобедренный (боковые стороны - ребра пирамиды). высота этого треугольника, проведенная к основанию - это высота пирамиды. обозначим ее н.

получаем а^2 = н*a*корень(2)/2; получается, что н тоже равно a*корень(2).

теперь надо найти апофемы боковых граней.

выберем какую-то сторону основания и проведем в боковой грани, её содержащей, апофему. проекция этой апофемы перпендикулярна этой стороне, потому что лежит в плоскости, которая перпендикулярна этой стороне - а именно, плоскости, в которой лежат апофема и высота пирамиды (каждая из этих прямых перпендикулярна этой стороне). следовательно, апофема является гипотенузой в прямоугольном треугольнике, образованной высотой пирамиды и отрезком, выходящим из центра квадрата в основании и препендикулярным стороне. такой отрезок, очевидно, равен а/2. легко сосчитать, что апофема m равна

m = a*корень(2 + 1/4) = a*корень(9/4) = а*3/2.

площадь боковой грани составит m*a/2 = a^2*3/4, всего боковых граней 4.

ответ. боковая поверхность равна 3*a^2

пожирательзнаний1

Геометрия

4,8(38 оценок)

a=16 см , b= 30 см , c=34 см

Проверим по теореме Пифагора, будет ли треугольник прямоугольным.

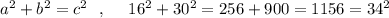
$a^2+b^2=c^2\ \ ,\ \ \ \ 16^2+30^2=256+900=1156=34^2$

Треугольник прямоугольный , c=34 - гипотенуза .

Высота, опущенная из прямого угла равна 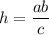$h=\dfrac{ab}{c}$ .

$h=\dfrac{16\cdot 30}{34}=\dfrac{8\cdot 30}{17}=\dfrac{240}{17}=14\dfrac{2}{17}$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.