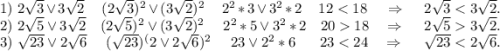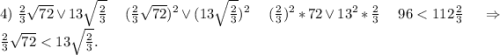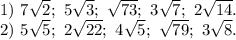Найти корни уравнения (6-x)(x-2)(3+x)(x+9) - 24x^=0 в ответ записать модуль их суммы.

158

454

Посмотреть ответы 2

Ответы на вопрос:

unucozi

Алгебра

4,8(13 оценок)

сводим к

-x^4-4x^3+33x^2+72x-324 = 0

324 = 2*2*3*3*3*3 это для подбора корней по теореме виета

заранее извесно что -9, -3, 2, 6 корнями не являются (это видно из изначального вида уравнения)

методом подбора узнаем что подходят такие корни -6, 3

делим все уравнение на (x+6)(x-3):

-x^2-x+18=0

d=73

x=(-1+-root(73))/2

поскольку все корни дествительные, то по теореме виета модуль их суммы это второй коэфициент в уравнении 4

если так посмотреть, то вообще корни искать и не надо было. мы только убедились что они действительные, а не комплексные

Retrica2002

Алгебра

4,7(1 оценок)

Объяснение:

4.4.

$1)\ 2\sqrt{3}\vee3\sqrt{2}\ \ \ \ (2\sqrt{3})^2\vee(3\sqrt{2})^2\ \ \ \ 2^2*3\vee3^2*2\ \ \ \ 123\sqrt{2}.\\3)\ \sqrt{23} \vee2\sqrt{6} \ \ \ \ (\sqrt{23} )^(2\vee2\sqrt{6})^2\ \ \ \ 23\vee2^2*6\ \ \ \ \ 23$

$4)\ \frac{2}{3}\sqrt{72}}\vee13\sqrt{\frac{2}{3} } \ \ \ \ (\frac{2}{3}\sqrt{72}})^2\vee(13\sqrt{\frac{2}{3} })^2\ \ \ \ (\frac{2}{3} )^2*72\vee13^2*\frac{2}{3}\ \ \ \ 96$

4.5.

$1)\ 7\sqrt{2};\ 5\sqrt{3} ;\ \sqrt{73};\ 3\sqrt{7};\ 2\sqrt{14}.\\ 2)\ 5\sqrt{5};\ 2\sqrt{22};\ 4\sqrt{5} ;\ \sqrt{79};\ 3\sqrt{8} .$

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.