екатерина24131

26.12.2020 07:11

Геометрия

Есть ответ 👍

Начерти прямоугольник со сторонами 4см и 3см.найдите его периметр.начерти квадрат,имеющий такой же периметр.

297

326

Посмотреть ответы 3

Ответы на вопрос:

armate

Геометрия

4,7(86 оценок)

Ну вот чертишь прямоугольник длинной 4 см и шириной 3 см 1) (4+3)*2=14(см)-периметр 2)14: 4=3,5(см)-сторона квадрата ну а дальше чертишь квадрат со стороной 3,5 по пойму так.

rejngardtdiana

Геометрия

4,6(94 оценок)

Прямоугольник сам сделай 1) (4*2)+(3*2)= 14 (см) периметр прямоугольника 2) 14: 4=3,5 (см) одна сторона квадрата рисуй квадрат со сторанами 3,5 см

Ульяна2732

Геометрия

4,6(64 оценок)

25. 7 : 8

Объяснение:

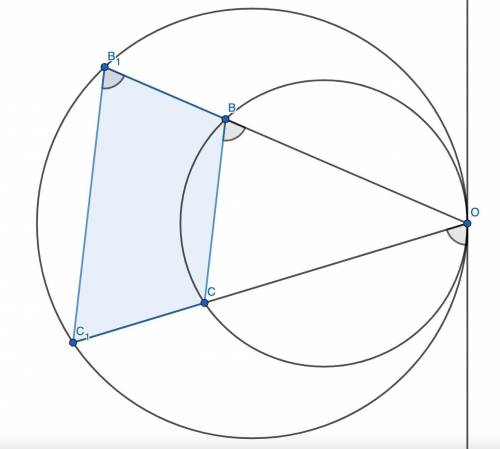
24. Проведём общую касательную к окружностям в точке O. Для меньшей окружности угол между касательной и хордой OC равен половине дуги OC, то есть равен вписанному углу ∠OBC. Для большей окружности угол между касательной и хордой OC₁ равен половине дуги OC₁, то есть равен вписанному углу ∠OB₁C₁. Поскольку хорды OC и OC₁ лежат на одной прямой, угол между касательной и этими хордами один и тот же. Углы ∠OBC и ∠OB₁C₁ равны одному и тому же углу, значит, они равны между собой. Тогда BC || B₁C₁.

По теореме синусов 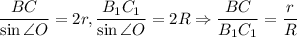$\dfrac{BC}{\sin{\angle{O}}}=2r,\dfrac{B_1C_1}{\sin{\angle{O}}}=2R\Rightarrow \dfrac{BC}{B_1C_1}=\dfrac{r}{R}$ . Поскольку радиусы не равны, то и BC ≠ B₁C₁.

Противолежащие стороны четырёхугольника параллельны и не равны, следовательно, это трапеция, что и требовалось доказать.

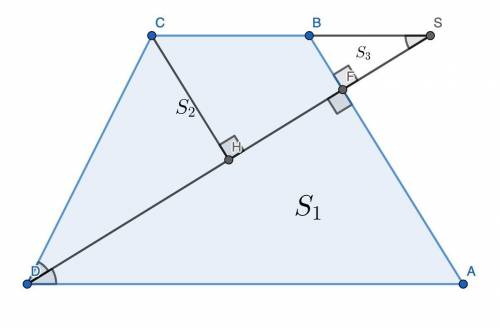
25. Продлим биссектрису DF до пересечения с прямой BC (точку пересечения обозначим S), проведём высоту CH в треугольнике DCS. Обозначим площади следующим образом: 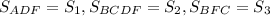$S_{ADF}=S_1,S_{BCDF}=S_2,S_{BFC}=S_3$ .

Заметим, что ∠ADS = ∠DSC как накрест лежащие, ∠ADS = ∠SDC по условию. Тогда ∠DSC = ∠SDC ⇒ треугольник DCS равнобедренный ⇒ DH = HS.

Треугольники ADF и BSF подобны по вертикальным углам ∠AFD и ∠BFS и накрест лежащим углам ∠ADF и ∠FSB с коэффициентом подобия k = AF : FB = 2. Тогда и DF : FS = 2, а 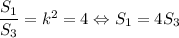$\dfrac{S_1}{S_3}=k^2=4\Leftrightarrow S_1=4S_3$ .

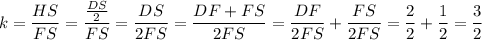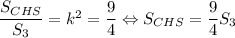Треугольники CHS и BFS подобны по общему углу ∠S и соответственным прямым углам ∠CHS и ∠BFS. Коэффициент подобия $k=\dfrac{HS}{FS}=\dfrac{\frac{DS}{2}}{FS}=\dfrac{DS}{2FS}=\dfrac{DF+FS}{2FS}=\dfrac{DF}{2FS}+\dfrac{FS}{2FS}=\dfrac{2}{2}+\dfrac{1}{2}=\dfrac{3}{2}$ . Тогда $\dfrac{S_{CHS}}{S_3}=k^2=\dfrac{9}{4}\Leftrightarrow S_{CHS}=\dfrac{9}{4}S_3$ .

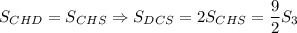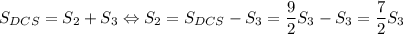CH — медиана треугольника DCS, значит, $S_{CHD}=S_{CHS}\Rightarrow S_{DCS}=2S_{CHS}=\dfrac{9}{2}S_3$ . Но $S_{DCS}=S_2+S_3\Leftrightarrow S_2=S_{DCS}-S_3=\dfrac{9}{2}S_3-S_3=\dfrac{7}{2}S_3$ .

Искомое отношение 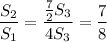$\dfrac{S_2}{S_1}=\dfrac{\frac{7}{2}S_3}{4S_3}=\dfrac{7}{8}$ .

Две задачи по геометрии ОГЭ 24.Окружности, радиусы которых равны r и R, касаются внутренним образом

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.