Пятизначное число назовем неразложимым, если оно не раскладывается в произведение двух трехзначных чисел. какое наибольшее число неразложимых пятизначных чисел может идти подряд?

230

336

Посмотреть ответы 2

Ответы на вопрос:

polyaketoztt67

Математика

4,7(51 оценок)

Самое маленькое число, представимое в виде произведения двух трёхзначных чисел, это 100·100 = 10000. следующее такое число: 100·101 = 10100, поэтому числа 10001, 10002, 10099 – неразложимые. таким образом, указано 99 идущих подряд неразложимых пятизначных чисел. больше, чем 99 неразложимых чисел идти подряд не может: каждое сотое пятизначное число оканчивается на два нуля, значит, его можно представить в виде произведения трёхзначного числа на 100.

Aminabr

Математика

4,8(28 оценок)

#125.

а). Пусть S₁ - площадь треугольной стороны, S₂ - прямоугольной стороны, а S₃ - основания (стороны, на которой лежит призма).

S₁ = 1/2 * 8 * 12 = 48 см²;

S₂ = 10 * 15 = 150 см²;

S₃ = 12 * 15 = 180 см².

S = 2S₁ + 2S₂ + S₃

S = 2*48 + 2*150 + 180 = 576 см².

б). S₁ = 1/2 * 3 * 8 = 12 см²;

S₂ = 22 * 5 = 110 см²;

S₃ = 22 * 8 = 176 см²;

S = 2S₁ + 2S₂ + S₃

S = 2*12 + 2*100 + 176 = 400 см².

#126.

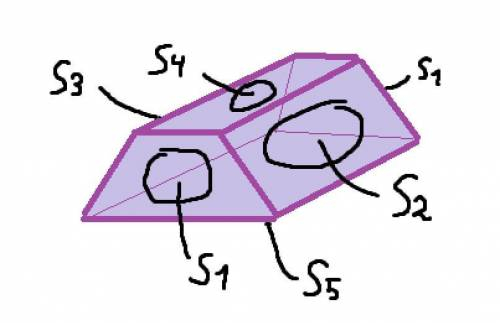
Пусть S₁ - площадь трапециевидной стороны, S₂ - площадь видимой прямоугольной боковой стороны, S₃ - площадь невидимой прямоугольной боковой стороны, S₄ - площадь прямоугольной стороны (сверху призмы), а S₅ - площадь основания. (Приложу картинку для лучшего понимания)

S₁ = (4 + 9)/2 * 5 = 32,5 см²;

S₂ = 5,7 * 20 = 114 см²;

S₃ = 5,5 * 20 = 110 см²;

S₄ = 4 * 20 = 80 см²;

S₅ = 9 * 20 = 180 см².

S = 2S₁ + S₂ + S₃ + S₄ + S₅

S = 65 + 114 + 110 + 80 + 180 = 549 см².

ОЧЕНЬ НУЖНО. не разобралась в этой теме решить эти 2 номера. сдать до понедельника!

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.