Вправильной треугольной пирамиде ребро основания равно а, боковое ребро= 2а. найдите углы наклона боковых ребер и боковых граней к плоскости основания.

267

464

Посмотреть ответы 2

Ответы на вопрос:

Zopa43

Геометрия

4,4(36 оценок)

основание правильной четырехугольной пирамиды - правильный четырехугольник или квадрат. для того, чтобы найти площадь основания - надо найти длину стороны основания. диагональное сечение пирамиды - это треугольник, имеющий основанием диагональ квадрата, а сторонами - боковые ребра. пусть длина диагонали равна b, тогда длина стороны квадрата будет равна, по теореме пифагора a = b/sqrt(2) (нарисуйте квадрат - разделите его диагональю. диагональ - это гипотенуза, стороны - катеты). площадь треугольника - сечения пирамиды, равна: s1 = b*h/2, где h - высота пирамиды, т.к. пирамида правильная. высота пирамиды делит сечение на 2 прямоугольных треугольника, так что, по теореме пифагора: h = sqrt(25 - b^2/4) с другой стороны, площадь основания равна: s2 = a^2 приравнивая s1 = s2 и исключая h, находим: b^2/4 = b*sqrt(25 - b^2/4)/2 или b^2 = 2b*sqrt(25 - b^2/4) b = 2sqrt(25 - b^2/4) из этого уравнения находите диагональ b, а затем стороно а и площадь квадра s2. вот и все! удачи!

Х1ега1Х

Геометрия

4,8(40 оценок)

Объяснение:

Воспользуемся теоремой синусов:

NP/sin(M) = MP/sin(N)

20/sin(75) = x/sin(60) sin75 = sin(30+45) = $\frac{\sqrt{3} + 1 }{2\sqrt{2} }$

x = 10( $3\sqrt{2} - \sqrt{6}$ )

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.
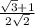
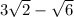