margarinfox

01.01.2021 03:10

Геометрия

Есть ответ 👍

Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 8 : 9, рахуючи від вершини кута при основі трикутника. знайдіть площу трикутника, якщо радіус вписаного кола дорівнює 16 см. *Підказка:потрібно записати кожну сторону в частинах, за теоремою Піфагора знайти скільки частин складає висота і повязати з радіусом

222

353

Посмотреть ответы 3

Ответы на вопрос:

vzarina576

Геометрия

4,6(37 оценок)

ответ:прости могут быть ошибки.И надеюсь все верно

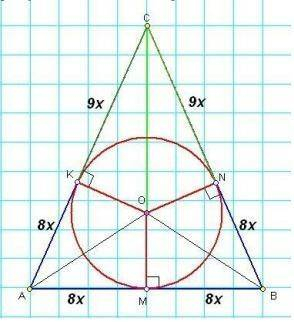
1) У рівнобедреному ΔАВС АС=ВС і СМ - висота, медіана та бісектриса,

ОМ - радіус вписаного кола, КА=АМ=NB=MB=8x, KC=CN=9x.

Площу трикутника можна знайти за формулою:

S=1/2AB*CM.

2) Розглянемо CMB - прямокутний.

По т.Піфагора знаходимо СМ=√(ВС²-ВМ²)=√((17х)²-(8х)²)=√(289х²-64х²)=

=√(225х²)=15х.

Оскільки центр вписаного кола - це точка перетину бісектрис, можна використовувати властивість бісектриси: b:c=b1:c1.

Використовуємо цю властивість для ΔСМВ та бісектриси ВО:

B:BM=CO:OM;

17x: 8x = CO: 16;

17:8 = CO: 16;

CO = 17 * 16 / 8 = 34 (см).

СМ = СО + ОМ = 34 +16 = 50 (см).

СМ = 15х = 50;

x = 50/15 = 10/3.

3) ABC: AB=16x=16*10/3=160/3 (см).

СМ = 50 см.

Знаходимо площу ΔАВС:

S=1/2*AB*CM=1/2*160/3*50=4000/3=1333 (см2).

Відповідь: 1333 см².

Объяснение:

Бічна сторона рівнобедреного трикутника точкою дотику вписаного кола ділиться у відношенні 8 : 9, ра

lidiyamartin9

Геометрия

4,5(66 оценок)

Обозначим длину равных сторон равнобедренного треугольника «х», а длину основания «2у».

Поскольку вписанный круг касается основания, расстояние от центра круга до основания равно высоте треугольника, которую мы назовем «h».

Используя теорему Пифагора, мы можем видеть, что:

h^2 + y^2 = x^2 (где x — гипотенуза прямоугольного треугольника, образованного высотой, половиной основания и одной из равных сторон)

Так как вписанная окружность касается боковой стороны треугольника, то расстояние от центра окружности до боковой стороны равно 16 см.

Назовем расстояние от вершины до точки разделения боковой стороны «а», а расстояние от этой точки до точки касания окружности «б».

Мы знаем, что a + b = x, и что b равно 9/17 длины боковой стороны, поэтому:

б = (9х)/(17)

а = х - б = (8х)/(17)

Теперь воспользуемся формулой площади треугольника:

Площадь = (1/2)bh

Подставляем найденные значения:

Площадь = (1/2)(2у)(ч)

ч ^ 2 + у ^ 2 = х ^ 2

а + б = х

б = (9х)/(17)

а = х - б = (8х)/(17)

ч = 16

Площадь = (1/2)(2г)(16)

Мы можем найти у, снова используя теорему Пифагора:

ч ^ 2 + у ^ 2 = х ^ 2

16^2 + у^2 = х^2

у ^ 2 = х ^ 2 - 256

у = кв (х ^ 2 - 256)

Теперь мы можем заменить y и упростить:

Площадь = (1/2)(2г)(16)

Площадь = 8 лет

Площадь = 8sqrt (x ^ 2 - 256)

Мы можем исключить x, используя соотношение между a, b и x:

а + б = х

(8х)/(17) + (9х)/(17) = х

17х/17 = х

х = 17

Теперь мы можем заменить x и найти площадь:

Площадь = 8sqrt (x ^ 2 - 256)

Площадь = 8кв.м (17^2 - 256)

Площадь = 8 кв.м. (145)

Площадь = 8 * 12,0416

Площадь = 96,3328 см ^ 2

Следовательно, площадь треугольника примерно равна 96,3328 см^2.

никита3343

Геометрия

4,6(99 оценок)

1)колышется-глагол(что делает? ) 2)н.ф.-колыхаться; признаки-пост,несов.в.,неперех.,возвр.,1спряжение; непост: в изъяв.накл.настоящее.вр.,единственно число 3)в предлож. является сказуемым. журч- корень, а, н- суф., е - окончание, основа - журчан

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Геометрия

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.