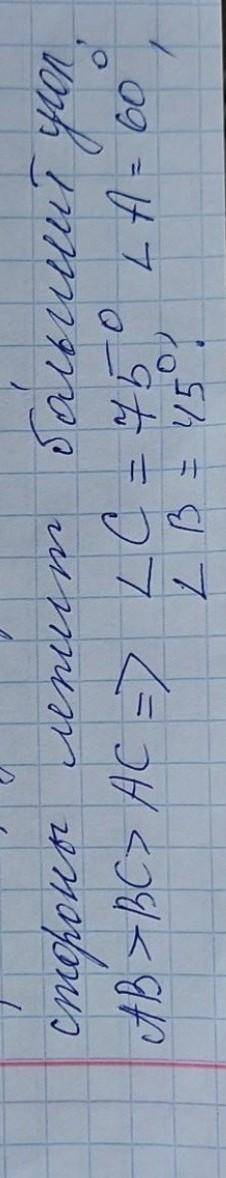Регистрация Спросить otvet5GPT
MrTroLoLo10
30.04.2023 13:37
Геометрия
Есть ответ 👍

В треугольнике ABC AB > BC > AC. Найдите ∠A,∠B,∠C, если известно, что один из углов треугольника равен 60°, а другой 45°

286
314
Посмотреть ответы 3

Ответы на вопрос:

Anglichanin228
Anglichanin228
4,5(95 оценок)

Объяснение:

Всё на фото


В треугольнике ABC AB > BC > AC. Найдите ∠A,∠B,∠C, если известно, что один из углов треугольни
В треугольнике ABC AB > BC > AC. Найдите ∠A,∠B,∠C, если известно, что один из углов треугольни
Йошино1
Йошино1
4,4(51 оценок)

сумма углов=180° => 180-(60+45)=75° третий угол

значит ∠A = 60°∠B = 45°∠C = 75°

nadezhstepan20
nadezhstepan20
4,8(80 оценок)
Дано: сторона основания а = 3 см, угол  α = 30°. находим высоту h основания: h = a*cos30° = 3√3/2. проекция бокового ребра на основание равна (2/3)*h = (2/3)*(3√3/2) =  √3. высота н пирамиды равна:   н = ((2/3)*h)*tgα =  √3*(1/√3) = 1 см. площадь so основания равна so = a²√3/4 = 3²√3/4 = 9√3/4  ≈    3,897114 см² .периметр основания р = 3а = 3*3 = 9 см.находим апофему а, проекция которой на основание равна (1/3)h.(1/3)h = (1/3)*(3√3/2) = √3/2 см. a =  √(h² +( (1/3)h)²) =  √(1² + (√3/2)²) =  √(1 + (3/4)) =  √7/2  ≈   1,322876 см. площадь sбок боковой поверхности равна: sбок = (1/2)ра = (1/2)*9*(√7/2) = 9√7/4  ≈  5,95294.площадь s полной поверхности пирамиды равна: s = so + sбок = (9√3/4) + (9√7/4) = (9/4)(√3 +  √7)  ≈  9,198002.объём v пирамиды равен:   v = (1/3)so*h = (1/3)*(9√3/4)*1 = (3√3/4)  ≈    1,299038 см³.

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS