Математика: Y -3y=4e^-x Дифференциальное линейное уравнение. Решите

nusechka44

12.01.2022 13:45

Математика

Есть ответ 👍

Y'-3y=4e^-x Дифференциальное линейное уравнение. Решите

238

497

Посмотреть ответы 2

Ответы на вопрос:

likapak1

Математика

4,6(1 оценок)

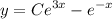
$\displaystyle y=Ce^{3x}-e^{-x}$

Пошаговое объяснение:

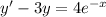
$y'-3y=4e^{-x}$

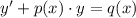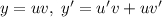Перед нами обычное линейное дифференциальное уравнение первого порядка вида $y'+p(x)\cdot y=q(x)$ . Решаются такие уравнения заменой $y=uv, \;y'=u'v+uv'$ .

Замена:

$\displaystyle u'v+uv'-3uv=4e^{-x}\\u'v+u(v'-3v)=4e^{-x}\\\left \{ {{v'-3v=0} \atop {u'v=4e^{-x}}} \right. \; \Leftrightarrow \; \left \{ {{ \frac{dv}{dx}=3v } \atop {u'v=4e^{-x}}} \right. \; \Leftrightarrow \;\left \{ {{ \frac{dv}{v}=3dx } \atop {u'v=4e^{-x}}} \right. \; \Leftrightarrow \;$

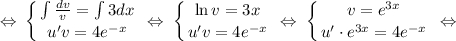
$\displaystyle \; \Leftrightarrow \;\left \{ {{ \int\limits { \frac{dv}{v} } =\int\limits {3dx} } \atop {u'v=4e^{-x}}} \right. \; \Leftrightarrow \;\left \{ {{\ln v=3x} \atop {u'v=4e^{-x}}} \right. \; \Leftrightarrow \;\left \{ {{v=e^{3x}} \atop {u'\cdot e^{3x}=4e^{-x}}} \right. \; \Leftrightarrow \;\\$

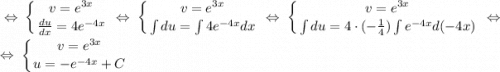
$\displaystyle \; \Leftrightarrow \;\left \{ {{v=e^{3x}} \atop { \frac{du}{dx}=4e^{-4x} }} \right. \; \Leftrightarrow \;\left \{ {{v=e^{3x}} \atop {\int\limits { du } = \int\limits {4e^{-4x}dx} }} \right. \; \Leftrightarrow \;\left \{ {{v=e^{3x}} \atop { \int\limits { du } = 4\cdot (-\frac{1}{4}) \int\limits {e^{-4x}d(-4x) }} \right. \; \Leftrightarrow \;\\\; \Leftrightarrow \;\left \{ {{v=e^{3x}} \atop {u=-e^{-4x}+C}} \right.$

Обратная замена:

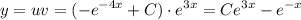
$\displaystyle y=uv=(-e^{-4x}+C)\cdot e^{3x}=Ce^{3x}-e^{-x}$

mrarmen1999mailru

Математика

4,4(5 оценок)

3arcsin(1/2) + 4arccos(-1/√2) – arctg(-√3)=3*π/6+4*(-3*π/π/3)=π/2-3*π+π/3=π*(1/2-3+1/3)=(5/6-3)*π=-13*π/6 ; вычислите: 2arcsin(-√3/2) + arctg(-1) + arccos(√2/2)=2*(-π/6 )+(-π/4 )+π/4=-π/3-π/4+π/4=-π/3 ;

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.