Регистрация Спросить otvet5GPT
Виолета131
18.10.2022 22:57
Математика
Есть ответ 👍

Точка М належить кулі з центром О і діаметром 8 см. Якою може бути відстань від точки М до точки О?

103
342
Посмотреть ответы 1

Ответы на вопрос:

Андріана1111111
Андріана1111111
4,5(16 оценок)

Пошаговое объяснение:

5.

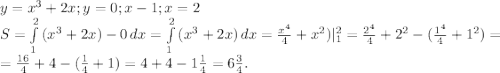
y=x^{3}+2x;y=0;x-1;x=2\\S=\int\limits^2_1 {(x^{3}+2x)-0 } \, dx =\int\limits^2_1 {(x^{3}+2x) } \, dx =\(\frac{x^{4} }{4}+x^{2} )|_1^2=\frac{2^{4} }{4} +2^{2}-(\frac{1^4}{4} +1^2)=\\=\frac{16}{4} +4-(\frac{1}{4} +1)=4+4-1\frac{1}{4} =6\frac{3}{4}.

ответ: S=6,75 кв. ед.

6.

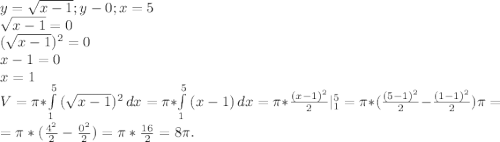
y=\sqrt{x-1} ;y-0;x=5\\\sqrt{x-1}=0\\(\sqrt{x-1} )^{2} =0\\x-1=0\\x=1\\V=\pi *\int\limits^5_1 {(\sqrt{x-1})^{2} } \, dx =\pi *\int\limits^5_1 {(x-1)} \, dx =\pi *\frac{(x-1)^{2} }{2}|_1^5 =\pi *(\frac{(5-1)^{2} }{2} -\frac{(1-1)^{2} }{2} )\pi =\\=\pi *(\frac{4^{2} }{2} -\frac{0^2}{2}) =\pi *\frac{16}{2} =8\pi .

ответ: V=25,133 куб. ед.

7.

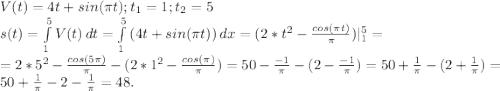
V(t)=4t+sin(\pi t);t_1=1;t_2=5\\s(t)=\int\limits^5_1 {V(t)} \, dt=\int\limits^5_1 {(4t+sin(\pi t)}) \, dx =(2*t^2-\frac{cos(\pi t)}{\pi } )|_1^5=\\ =2*5^2-\frac{cos(5\pi) }{\pi } -(2*1^2-\frac{cos(\pi) }{\pi} )=50-\frac{-1}{\pi } -(2-{\frac{-1 }{\pi } )}=50+\frac{1}{\pi } -(2+\frac{1}{\pi } )=50+\frac{1}{\pi } -2-\frac{1}{\pi } =48.}

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Математика

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS