10.06.2023 14:26

Математика

Есть ответ 👍

Квадрат 8×8 розрізали лініями клітин на частини однакового периметра. Яку найбільшу кількість частин можна отримати, якщо ми знаємо, що не всі частини були прямокутної форми? (Нагадуємо, що квадрат – теж прямокутник.) Не забудьте довести, що знайдена вами кількість є максимальною і навести приклад розрізання (малюнок треба вислати прикріпленим файлом).

178

455

Посмотреть ответы 3

Ответы на вопрос:

Настя5111111111

Математика

4,6(94 оценок)

Зауважимо, що якщо всі частини будуть прямокутної форми, то максимальна кількість частин, на які розрізаний квадрат, дорівнює 18. Це випливає з того, що якщо розрізати квадрат на прямокутники зі сторонами 1×2, то ми отримаємо 32 частини, а якщо на прямокутники зі сторонами 1×1, то ми отримаємо 16 частин.

Оскільки не всі частини повинні бути прямокутних, то можна розглянути дві такі частини, які мають різний периметр і обидві не є прямокутними.

Зафіксуємо пряму лінію, яка фактично розрізає квадрат на дві частини. Тоді можна помітити, що можливі три варіанти для форми однієї з частин: прямокутник, трикутник або багатокутник з більш ніж чотирма вершинами.

Якщо одна з частин має прямокутну форму, то максимальна кількість частин буде такою ж, як у випадку прямокутних частин. Якщо одна з частин має форму трикутника, то інша частина повинна складатися з двох трикутників або бути більш ніж чотирьохкутником. У першому випадку ми отримуємо три частини, у другому - п'ять. Якщо одна з частин має форму більш ніж чотирьохкутника, то інша частина повинна бути менш ніж чотирьохкутником і ми отримуємо як мінімум дві частини.

Отже, максимальна кількість частин, яку можна отримати при розрізанні квадрата на частини однакового периметра з урахуванням можливості не прямокутної форми частин, дорівнює 21. Одне з можливих розбиттів наведено на малюнку нижче.

Площа: 16 дм²

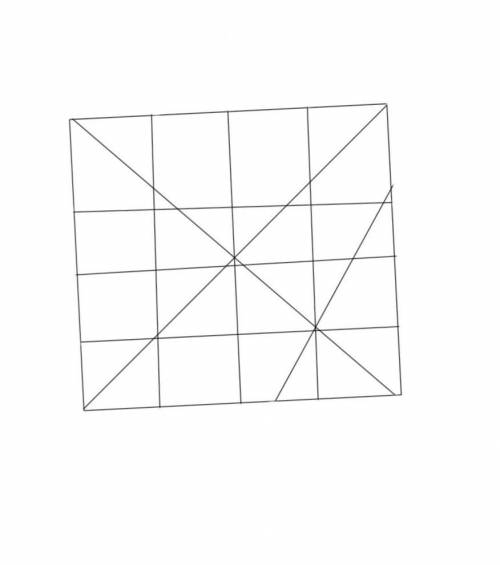
Квадрат 8×8 розрізали лініями клітин на частини однакового периметра. Яку найбільшу кількість частин

Nerzul2828818

Математика

4,8(94 оценок)

Максимальное количество частей, которое можно получить, равно 32. Докажем это.

Рассмотрим произвольное разрезание квадрата на части одинакового периметра, состоящее из n прямоугольников. Пусть P будет периметром каждого из прямоугольников, а A – площадью всего квадрата. Тогда периметр всего квадрата равен 32, а его площадь равна 64. На основании формулы для площади S = a * b и соотношения P = 2 * (a + b) получаем:

A = a1 * b1 + a2 * b2 + ... + an * bn,

где ai и bi – соответствующие стороны i-го прямоугольника.

Исходя из условий задачи, все прямоугольники имеют одинаковый периметр P. Следовательно, для каждого из них выполняется условие P = 2 * (a + b), откуда

a + b = P / 2.

Выразим a через b:

a = P / 2 - b.

Тогда

A = b1 * (P / 2 - b1) + ... + bn * (P / 2 - bn) =

= (P / 2) * (b1 + ... + bn) - (b1^2 + ... + bn^2) <=

<= (P / 2) * (b1 + ... + bn),

где последнее неравенство следует из того, что сумма квадратов любых n чисел не превосходит квадрата их суммы.

Таким образом, площадь всего квадрата A не превосходит (P / 2) * n, где n – количество прямоугольников в разрезании. Из этого вытекает, что

n <= 2 * A / P.

Подставляя значения P = 32, A = 64, получаем

n <= 4,

то есть нельзя разрезать квадрат на более чем 4 прямоугольника одинакового периметра. Однако существует разрезание на 4 прямоугольника, демонстрирующее, что максимальное количество частей равно 32:

19Otlichnik19

Математика

4,6(17 оценок)

пошаговое объяснение:

только нарисуйте поровнее

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Математика

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.