Алгебра: Представьте ввиде многочлена

MariyaPak2701

23.12.2021 14:03

Алгебра

Есть ответ 👍

Представьте ввиде многочлена

193

316

Посмотреть ответы 2

Ответы на вопрос:

saulefazylovnap00xfc

Алгебра

4,8(5 оценок)

Квадрат суммы нескольких слагаемых равен сумме квадратов этих слагаемых, сложенной со всевозможными удвоенными попарными произведениями этих слагаемых.

Схематично это можно записать так:

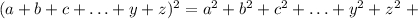
$(a+b+c+\ldots+y+z)^2=a^2+b^2+c^2+\ldots+y^2+z^2\ +$

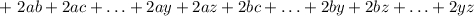
$+\ 2ab+2ac+\ldots+2ay+2az+2bc+\ldots+2by+2bz+\ldots+2yz$

Распишем четвертую степень как квадрат квадрата:

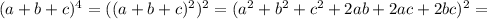
(a+b+c)^4=((a+b+c)^2)^2=(a^2+b^2+c^2+2ab+2ac+2bc)^2=

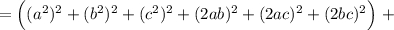
$=\Big((a^2)^2+(b^2)^2+(c^2)^2+(2ab)^2+(2ac)^2+(2bc)^2\Big)\ +$

$+\ \Big(2\cdot a^2\cdot b^2+2\cdot a^2\cdot c^2+2\cdot a^2\cdot 2ab+2\cdot a^2\cdot 2ac+2\cdot a^2\cdot 2bc\Big)\ +$

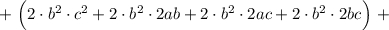
$+\ \Big(2\cdot b^2\cdot c^2+2\cdot b^2\cdot 2ab+2\cdot b^2\cdot 2ac+2\cdot b^2\cdot 2bc\Big)\ +$

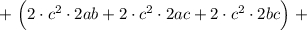
$+\ \Big(2\cdot c^2\cdot 2ab+2\cdot c^2\cdot 2ac+2\cdot c^2\cdot 2bc\Big)\ +$

$+\ \Big(2\cdot 2ab\cdot 2ac+2\cdot2ab\cdot 2bc\Big)+\Big(2\cdot2ac\cdot 2bc\Big)=$

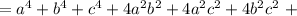
$=a^4+b^4+c^4+4a^2b^2+4a^2c^2+4b^2c^2\ +$

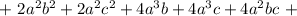
$+\ 2a^2b^2+2a^2c^2+4a^3b+4a^3c+4a^2bc\ +$

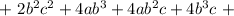
$+\ 2b^2c^2+4ab^3+4ab^2c+4b^3c\ +$

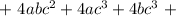
$+\ 4abc^2+4ac^3+4bc^3\ +$

$+\ 8a^2bc+8ab^2c+8abc^2=$

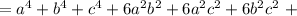
$=a^4+b^4+c^4+6a^2b^2+6a^2c^2+6b^2c^2\ +$

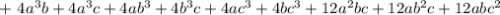
$+\ 4a^3b+4a^3c+4ab^3+4b^3c+4ac^3+4bc^3+12a^2bc+12ab^2c+12abc^2$

Зюна

Алгебра

4,6(35 оценок)

Выбирают 1 девочку из 5-ти (число сочетаний из 5 по 1)и 1 мальчика из 4-х (число сочетаний из 4 по одному): . 2 способ. количество способов выбрать одну девочку = 5, количество способов выбрать одного мальчика = 4. по правилу произведения 5*4=20.

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

наталья763
09.03.2020 12:37

Постройте график уровнения 26 y=x+5 y=x-4 y=7-2x...
pashahitman1900
28.11.2022 04:18

Найди значение выражения x2+2x√3+10 , если x=√3+1 побыстрей...
MsMerenberg86
02.07.2022 14:54

Найдите корни квадратных трёхчленов. 1)х²-7х; 2)х²-7; 3)3х²-27;...
AnnI820
02.10.2020 19:43

4sin pi * cos pi + tg pi -ctg 3pi/2...
kkatya3082
13.01.2020 01:38

Известно,что 4x2y5=3. найти значение выражения: -20x4y10...
Anastasia12578
20.10.2020 08:44

Вычислите производную функции y=tgx⋅(x−2) при x=0...
urasaya
21.01.2022 04:31

1. Укажите соответствующий вывод для каждого неравенства. Обоснуйте...
glushkovaov
02.02.2021 13:27

6 arcsin( x2 -6x + 8,5) =п...
vlad200883
19.04.2020 17:18

7. Упростите выражение: - + 2 a b, b 0, ab...
Olga6491
22.04.2021 02:25

Решение неравенство постройте на кординатной плоскости х2+у...

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.