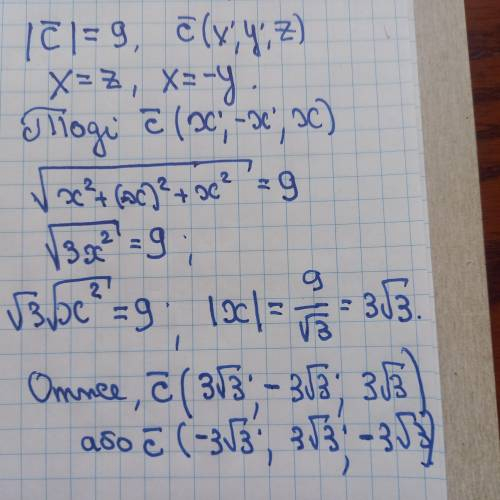Регистрация Спросить otvet5GPT
rimolol
20.12.2020 07:23
Геометрия
Есть ответ 👍

Модуль вектора c̅ (x; y; z) дорівнює 9, його координати x і z є рівними, а координати x і y — протилежні числа. Знайдіть координати вектора c̅ .

252
488
Посмотреть ответы 3

Ответы на вопрос:

vadimsheglov0
vadimsheglov0
4,6(70 оценок)

Відповідь:

Дано, що модуль вектора c̅ дорівнює 9, тобто ||c̅|| = 9.

Також, за умовою, координати x і z вектора c̅ є рівними, тобто x = z.

Координати x і y є протилежними числами, тобто x = -y.

Ми можемо використати формулу модуля вектора, яка виглядає наступним чином:

||c̅|| = sqrt(x^2 + y^2 + z^2),

де sqrt позначає квадратний корінь.

Підставляючи відомі значення, отримуємо:

9 = sqrt((-y)^2 + y^2 + x^2).

Спрощуючи це рівняння, отримуємо:

9 = sqrt(2y^2 + x^2).

Квадратуючи обидві частини рівняння, отримуємо:

81 = 2y^2 + x^2.

Ми маємо ще дві рівності: x = z і x = -y. Підставляючи ці значення в останнє рівняння, отримуємо:

81 = 2(-y)^2 + (-y)^2.

Спрощуючи це рівняння, отримуємо:

81 = 2y^2 + y^2.

81 = 3y^2.

Ділимо обидві частини рівняння на 3:

27 = y^2.

Звідси випливає, що y = ±√27.

Враховуючи, що x = -y, ми отримуємо:

x = -√27 і x = √27.

Таким чином, координати вектора c̅ будуть:

c̅ (x, y, z) = (-√27, ±√27, -√27) і c̅ (x, y, z) = (√27, ±√27, √27), де ± вказує на два можливих напрямки координати y.

Пояснення:

Andezia
Andezia
4,4(65 оценок)

Відповідь: фото

Пояснення:




Модуль вектора c̅ (x; y; z) дорівнює 9, його координати x і z є рівними, а координати x і y — протил
akm0910
akm0910
4,8(40 оценок)

ответ:

на фото

объяснение:

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS