Регистрация Спросить otvet5GPT
Krasotcakotik
16.09.2022 13:03
Геометрия
Есть ответ 👍

На рисунку точка O — центр вписаного кола трикутника ABC. Знайдіть кут ACB, якщо кут AOB дорівнює 140°, з поясненням, будь ласка! ів

291
449
Посмотреть ответы 3

Ответы на вопрос:

zlatinovaangel
zlatinovaangel
4,7(42 оценок)

ответ.

ΔАВС , О - центр вписанной окружности , ∠АОВ = 140° .

Центр вписанной окружности лежит на пересечении биссектрис углов .

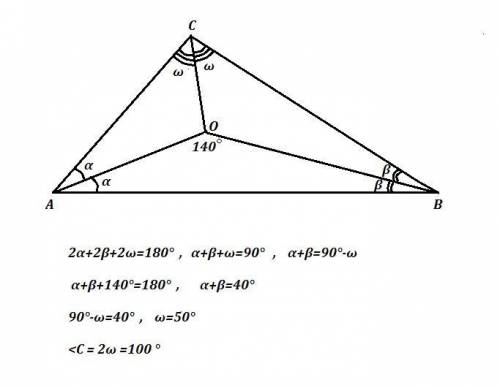
Обозначим  ∠А=2α  ,  ∠В=2β  ,  ∠С=2ω .

Тогда ∠САО=∠ВАО=α  ,  ∠АВО=∠СВО=β  ,  ∠АСО=∠ВСО=ω  .

Сумма углов треугольника равна 180° , поэтому

∠А+∠В+∠С=2α+2β+2ω=180°   ⇒    α+β+ω=90°  ,  α+β=90°-ω  (*)

Из  ΔАОВ имеем:   ∠АОВ+α+β=180°  ,   140°+α+β=180°  ,  

α+β=180°-∠АОВ=180°-140°=40°    (**)  

Приравняем правые части равенств (*)  и  (**) .        

90°-ω=40°

90°-40°=ω

ω=50°

2ω=100°

∠АСВ=100°


На рисунку точка O — центр вписаного кола трикутника ABC. Знайдіть кут ACB, якщо кут AOB дорівнює 14
aresu
aresu
4,4(50 оценок)

∠ACB = 100°

Объяснение:

На рисунку точка O — центр вписаного кола трикутника ABC. Знайдіть кут ACB, якщо кут AOB дорівнює 140°

Центр кола, вписаного в трикутник, є точкою перетину його бісектрис.Розв'язання

Нехай АВС - даний трикутник. ∠AOB=140°. Знайдемо ∠ACB.

1) Так як суму кутів трикутника дорівнює 180°, то в ΔAOB:

∠ОАВ+∠ОВА=180°-∠АОВ=180°-140°=40°

2) Так як  O — центр вписаного кола трикутника ABC, то АО і ВО - бісектриси кутів САВ і СВА відповідно. Отже за означенням бісектриси кута трикутника маємо:

∠САВ=2·∠ОАВ

∠СВА=2·∠ОВА

Тоді їх сума:

\sf \angle CAB+\angle CBA=2\cdot \angle OAB+2\cdot\angle OBA=2\cdot (\underset{40^\circ}{\underbrace{\angle OAB+\angle OBA})}=\bf 80^\circ

3) У ΔАВС за теоремою про суму кутів трикутника знайдемо кут АСВ:

∠АСВ=180°-(∠САВ+∠СВА)=180°-80°= 100°

Відповідь: А. 100°

zakir2007
zakir2007
4,5(63 оценок)
Прямоугольный параллелепипед, описанный около сферы - есть куб со стороной, равной двум радиусам. а = 5 объём куба равен: v = a³ = 5³ = 125

Реши свою проблему, спроси otvet5GPT

  • Быстро
    Мгновенный ответ на твой вопрос
  • Точно
    Бот обладает знаниями во всех сферах
  • Бесплатно
    Задай вопрос и получи ответ бесплатно

Популярно: Геометрия

Caktus Image

Есть вопросы?

  • Как otvet5GPT работает?

    otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.

  • Сколько это стоит?

    Проект находиться на стадии тестирования и все услуги бесплатны.

  • Могу ли я использовать otvet5GPT в школе?

    Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!

  • В чем отличия от ChatGPT?

    otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.

Подпишись на наш телеграмм канал

GTP TOP NEWS