Алгебра: Розв яжіть систему нерівностей

глупенький11

18.06.2022 14:28

Алгебра

Есть ответ 👍

Розв'яжіть систему нерівностей

119

429

Посмотреть ответы 2

Ответы на вопрос:

2зик20

Алгебра

4,4(68 оценок)

Множество решений системы неравенств (-∞; 0)

Объяснение:

Перевод: Решите систему неравенств

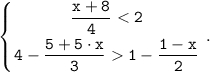
$\displaystyle \tt \left \{ {{\dfrac{x+8}{4} < 2} \atop {4-\dfrac{5+5 \cdot x}{3} 1-\dfrac{1-x}{2} }} \right. .$

Информация: Если a > b (или a < b), c > 0, то a·c > b·c (или a·c < b·c).

Решение. Обе части первого уравнения умножим на положительное число 4, а обе части второго уравнения умножим на положительное число 6=3·2, а потом упростим.

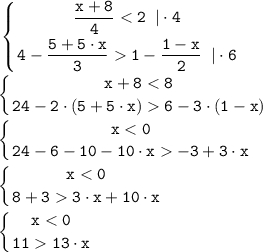
$\displaystyle \tt \left \{ {{\dfrac{x+8}{4} < 2 \;\; | \cdot 4} \atop {4-\dfrac{5+5 \cdot x}{3} 1-\dfrac{1-x}{2} } \;\; | \cdot 6} \right. \left \{ {{x+8 < 8} \atop {24-2 \cdot (5+5 \cdot x) 6-3 \cdot (1-x) } \right. \left \{ {{x < 0} \atop {24-6-10-10 \cdot x -3 +3 \cdot x } \right. \left \{ {{x < 0} \atop {8+3 3 \cdot x+10 \cdot x } \right. \left \{ {{x < 0} \atop {11 13 \cdot x } \right.$

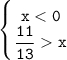
$\displaystyle \tt \left \{ {{x < 0} \atop {\dfrac{11}{13} x } \right.$

Определим множество решений каждого неравенства:

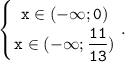
$\displaystyle \tt \left \{ {{x \in (-\infty; 0)} \atop {x \in (-\infty; \dfrac{11}{13} ) } \right. .$

Так как рассматривается система, то находим пересечение множеств решений:

x ∈ (-∞; 0).

#SPJ1

resetmac

Алгебра

4,6(65 оценок)

Xмест в каждом ряду 2-го залах+4 мест в каждом ряду 1-го зала12*(x+4) + 15x = 53412x + 48 + 15х = 53427x = 486х = 486: 27 = 1818*15=270 мест во 2-м зале534-270=264 места в 1-м зале

Реши свою проблему, спроси otvet5GPT

Быстро
Мгновенный ответ на твой вопрос
Точно
Бот обладает знаниями во всех сферах
Бесплатно
Задай вопрос и получи ответ бесплатно

Задай свой вопрос

Популярно: Алгебра

Есть вопросы?

Как otvet5GPT работает?

otvet5GPT использует большую языковую модель вместе с базой данных GPT для обеспечения высококачественных образовательных результатов. otvet5GPT действует как доступный академический ресурс вне класса.
Сколько это стоит?

Проект находиться на стадии тестирования и все услуги бесплатны.
Могу ли я использовать otvet5GPT в школе?

Конечно! Нейросеть может помочь вам делать конспекты лекций, придумывать идеи в классе и многое другое!
В чем отличия от ChatGPT?

otvet5GPT черпает академические источники из собственной базы данных и предназначен специально для студентов. otvet5GPT также адаптируется к вашему стилю письма, предоставляя ряд образовательных инструментов, предназначенных для улучшения обучения.